Cap. 10 Parcela subdividida

No delineamento em parcelas subdivididas existem dois tipos de tratamento: o principal e o secundário. As parcelas são subdivididas no espaço, ou no tempo. Depois que os tratamentos principais (parcelas) são sorteados, sorteia-se o tratamento secundário (subparcelas) dentro das parcelas.

Indica-se o uso de parcelas subdivididas quando:

A parcela é uma “unidade” que pode receber vários tratamentos secundários. No setor florestal esta unidade pode ser um vaso, ou mesmo uma árvore.
Não é possível instalar o experimento no esquema fatorial.
O tratamento principal exige parcelas custosas, seja do ponto de vista financeiro ou do esforço.
A busca pela precisão está no tratamento secundário.
Deseja-se que a variação entre subparcelas seja menor que entre as parcelas.

O modelo estatístico do delineamento em parcela subdividida é:

\[Y = \bar{Y} + BLOCO + TRAT_A + Erro_{Parcela} + TRAT_B + (TRAT_A * TRAT_B) + Erro_{Subparcela}\]

10.1 O caso balanceado

Como exemplo de um desenho de parcela subdividida balanceado, tem-se um experimento de regeneração natural do sub bosque de três formações florestais. Nas parcelas de cada uma das área naturais estudadas, implantaram-se subparcelas correspondendo a três alturas de desrama. O efeito dos tratamentos foi medido através do número de indivíduos regenerantes.

Fator na parcela: Floresta A, B e C
Fator nas subparcelas: Desrama a 2, 5 e 7 metros
3 repetições
Variável de interesse: número de indivíduos regenerantes

Table 10.1: Dados de experimento em parcela subdividida
floresta	rep	desrama	indiv
A	1	2	48
A	2	2	47
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	101
A	2	7	105
A	3	7	112
B	1	2	90
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	2	2	101
C	3	2	103
C	1	5	130
C	2	5	133
C	3	5	140
C	1	7	144
C	2	7	147
C	3	7	148

O primeiro passo é importar o arquivo contendo os resultados do experimento para dentro do R. Esta tarefa pode ser realizada através do seguinte comando:

sub = read.csv("./data/Experimento Subdividida.csv", 
               sep = ",", dec = ".")

Você já sabe! Antes de ir para análise estatística explore graficamente os dados.

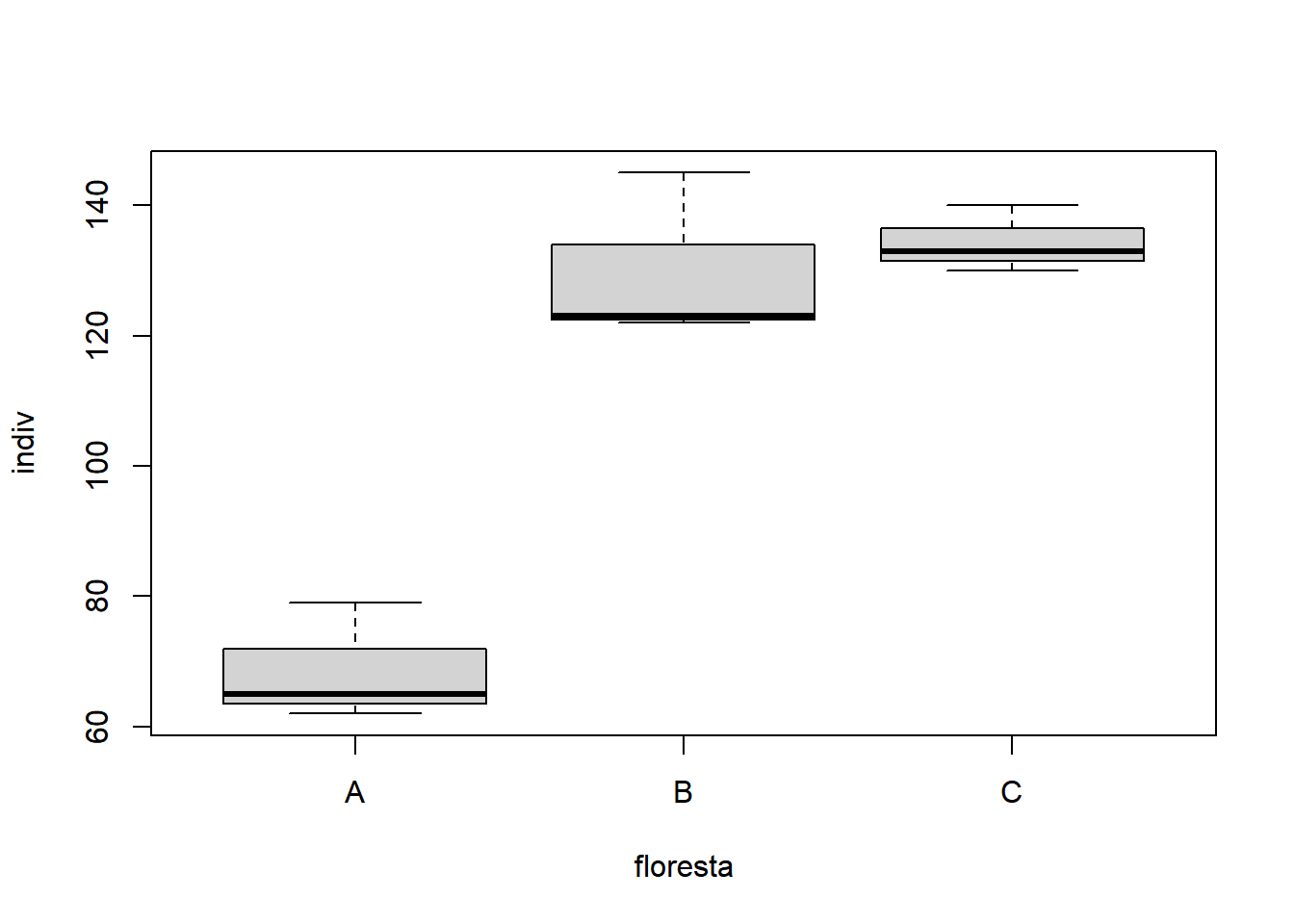
Considerando apenas tratamento principal:

boxplot(data = sub, indiv ~ floresta)

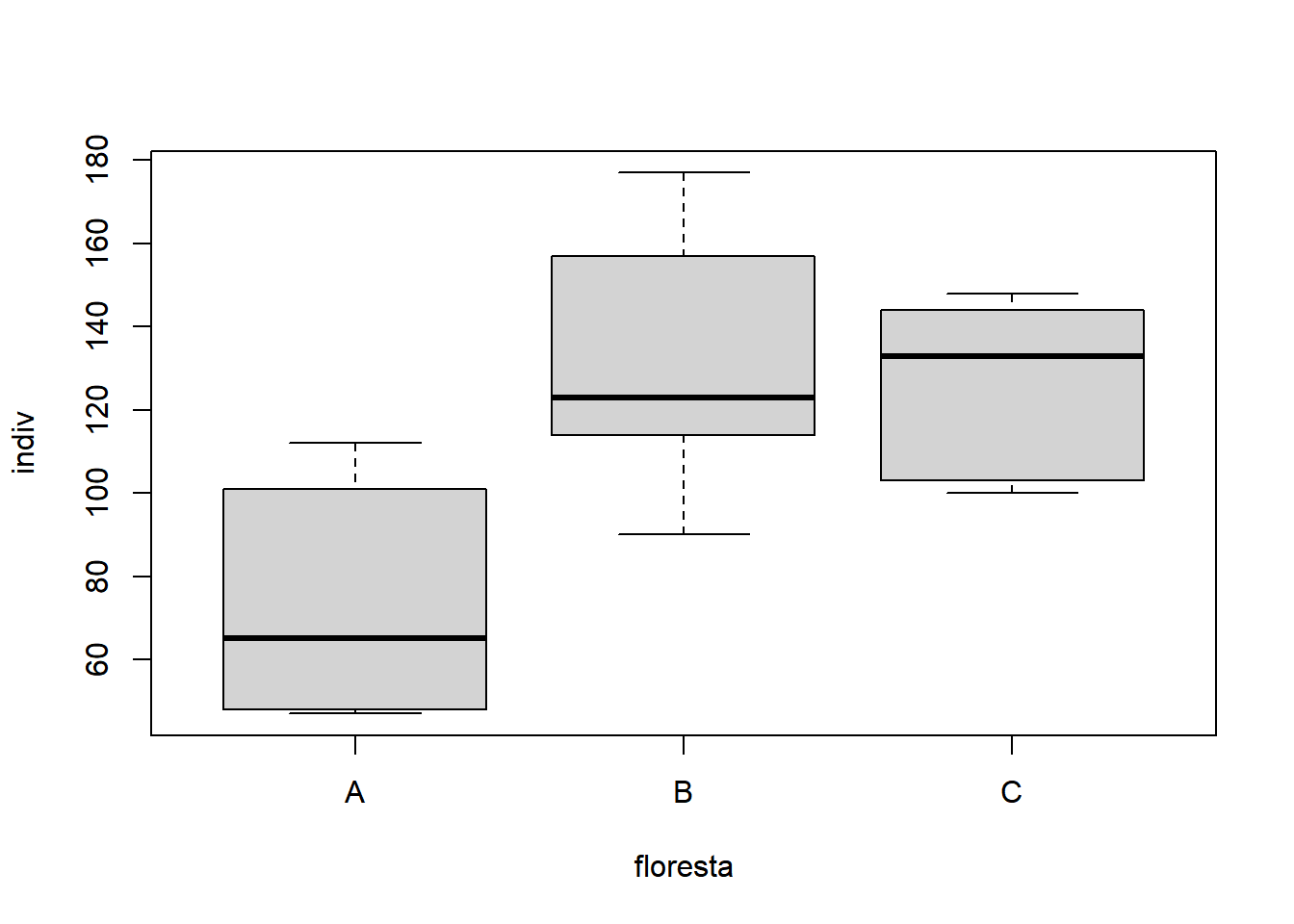
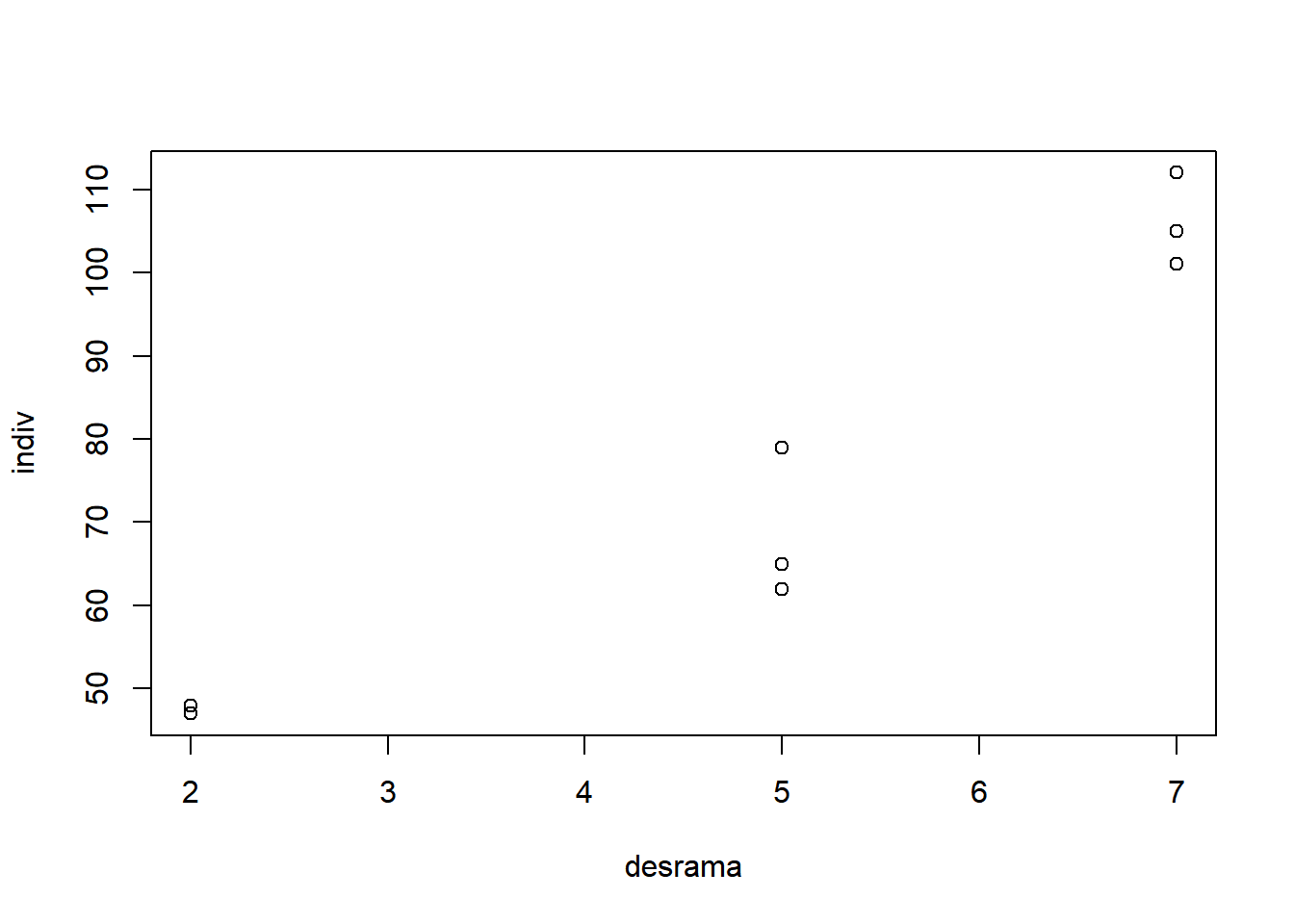
Considerando apenas tratamento secundário:

plot(data = sub, indiv ~ desrama)

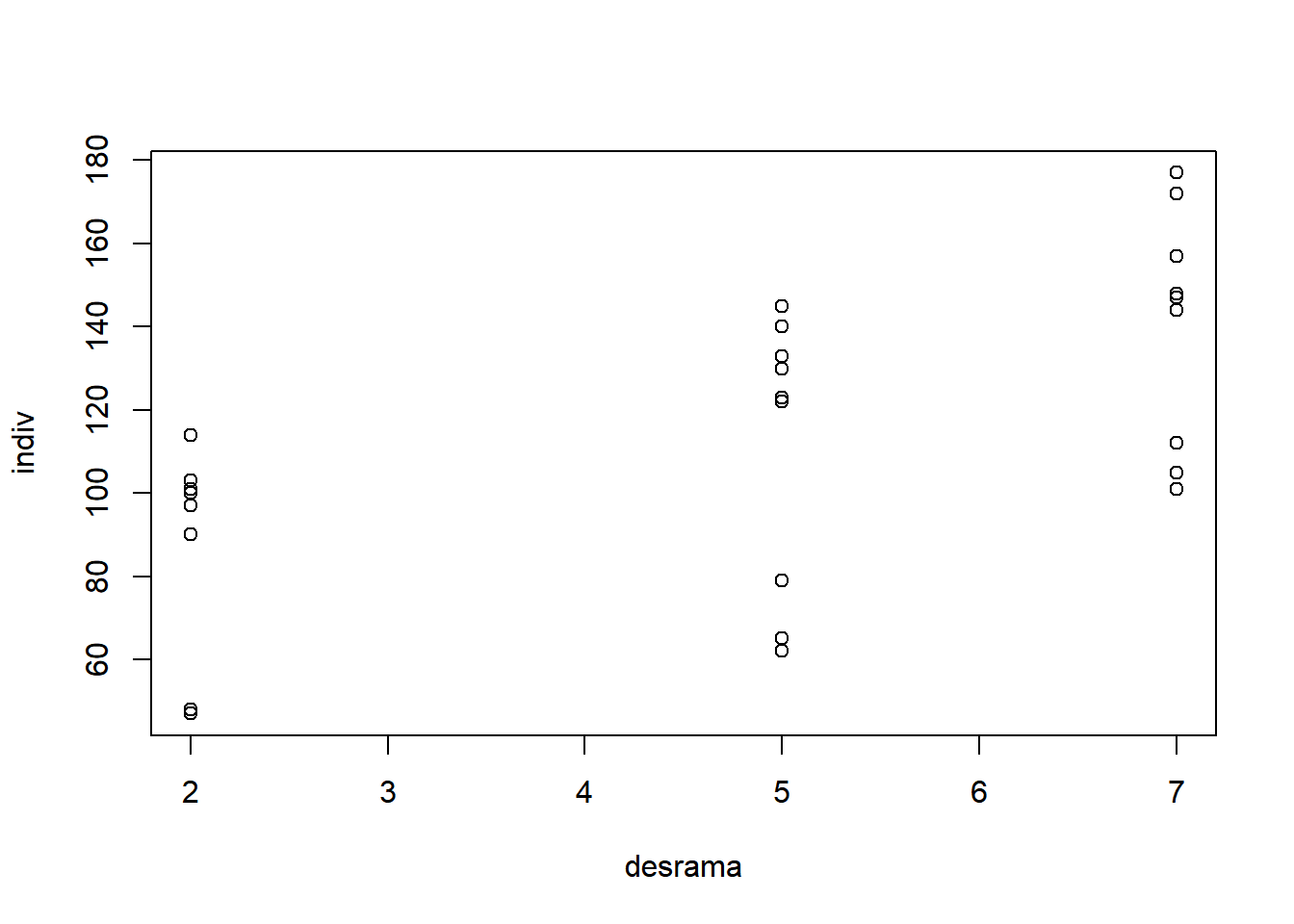
Interação dos tratamentos:

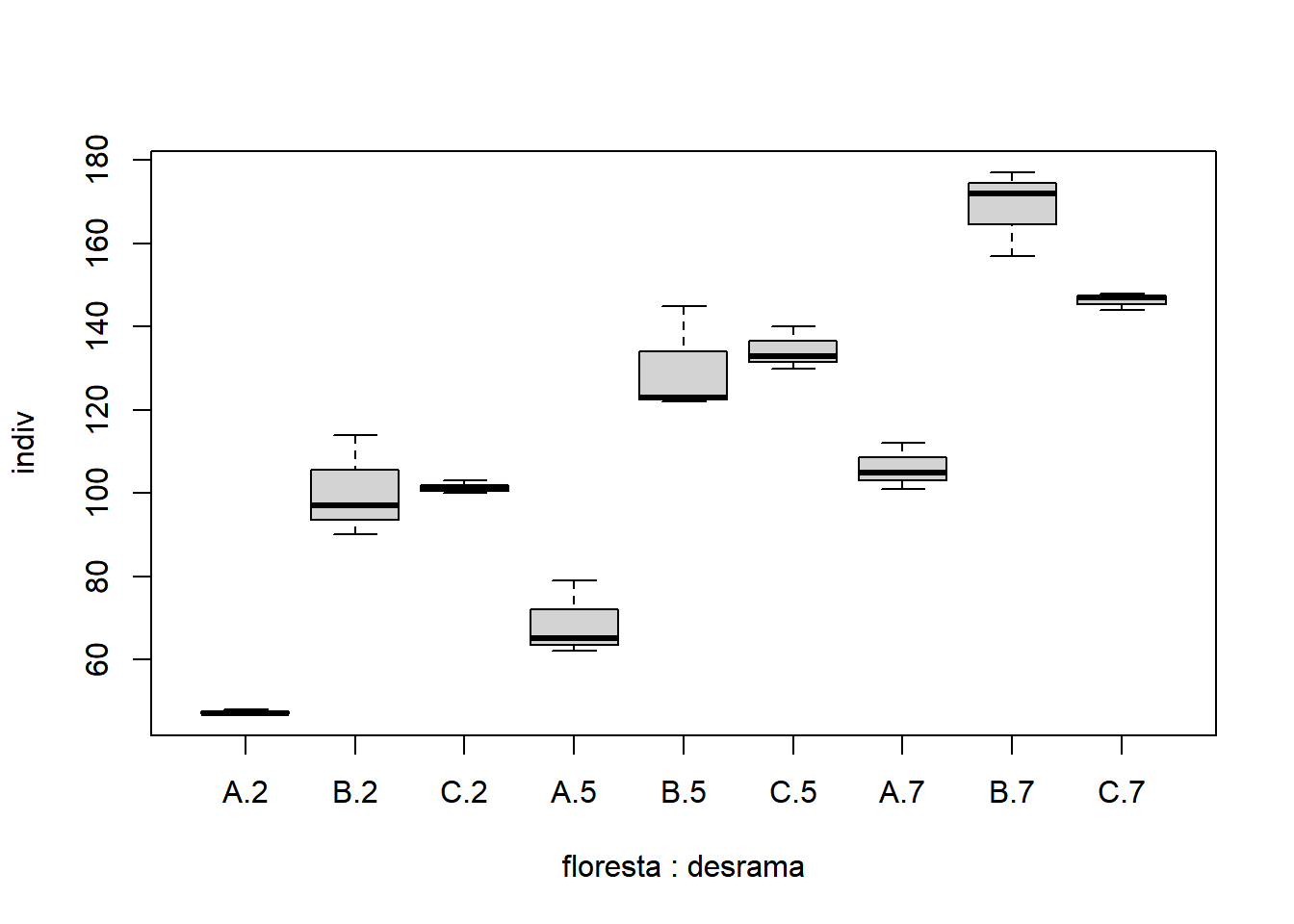
boxplot(data = sub, indiv ~ floresta/desrama)

Fixando desrana até 2 metros:

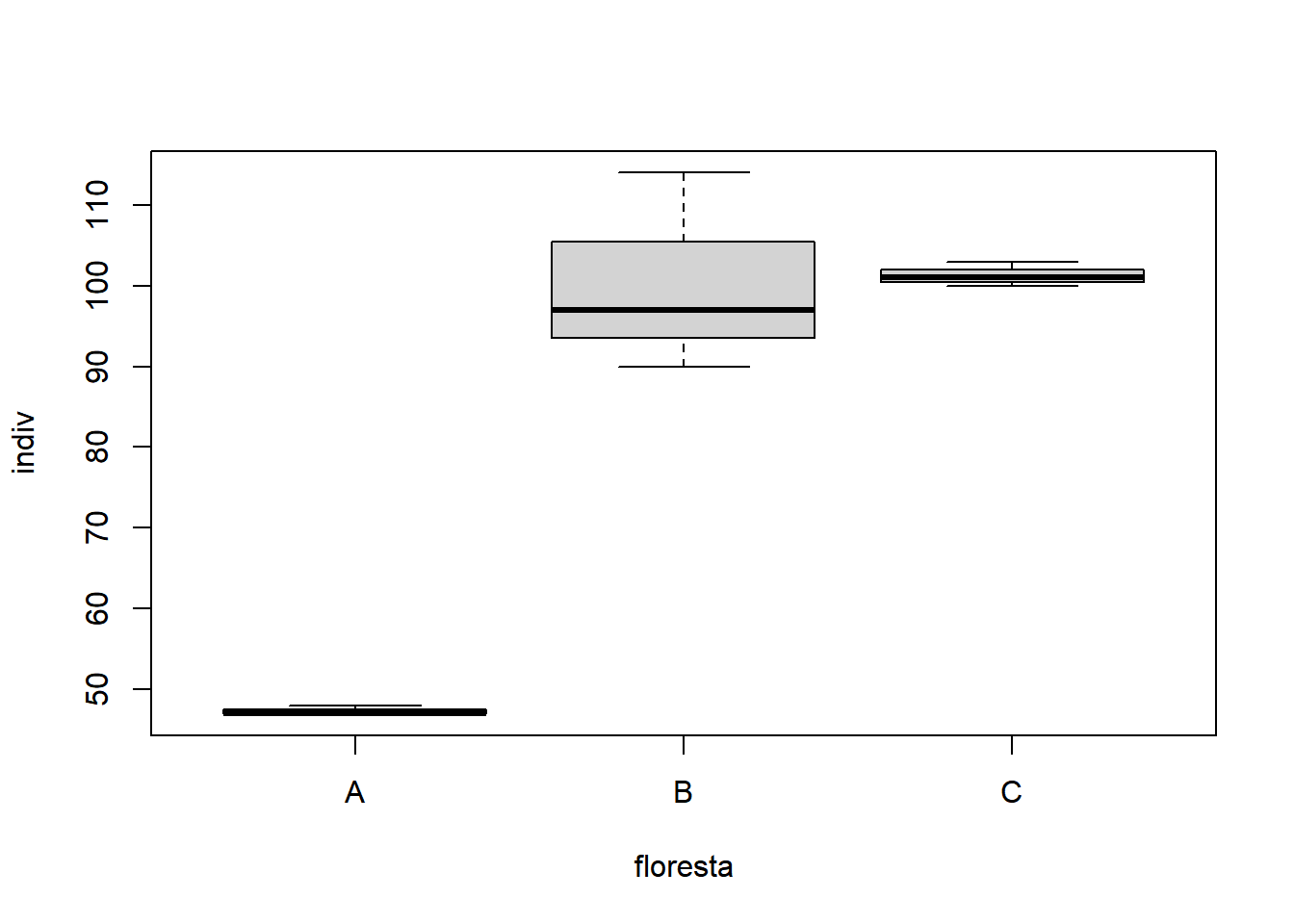
boxplot(data = sub[sub$desrama == 2,], indiv ~ floresta)

Fixando desrana até 5 metros:

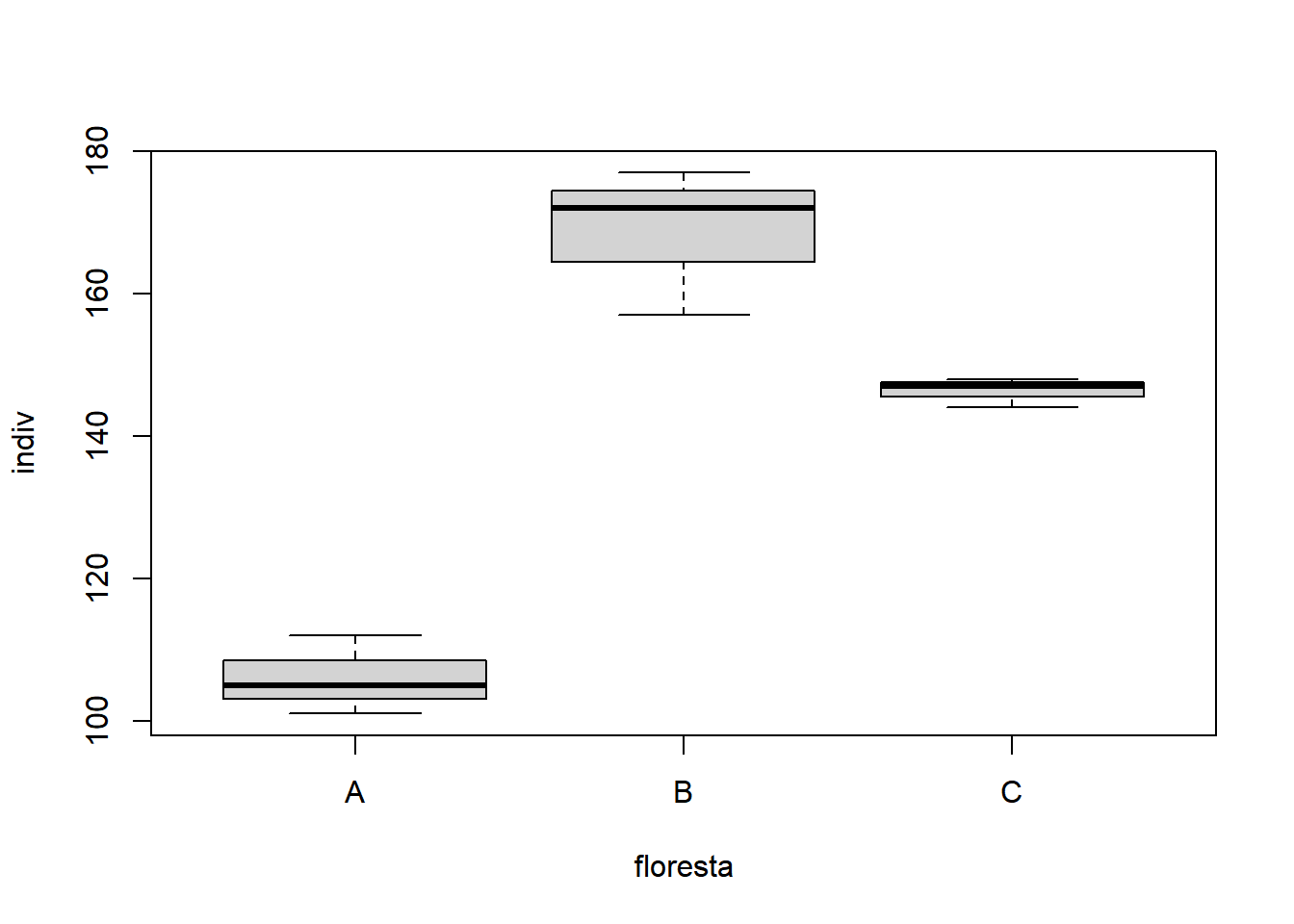
boxplot(data = sub[sub$desrama == 5,], indiv ~ floresta)

Fixando desrana até 7 metros:

boxplot(data = sub[sub$desrama == 7,], indiv ~ floresta)

Fixando floresta igual a A:

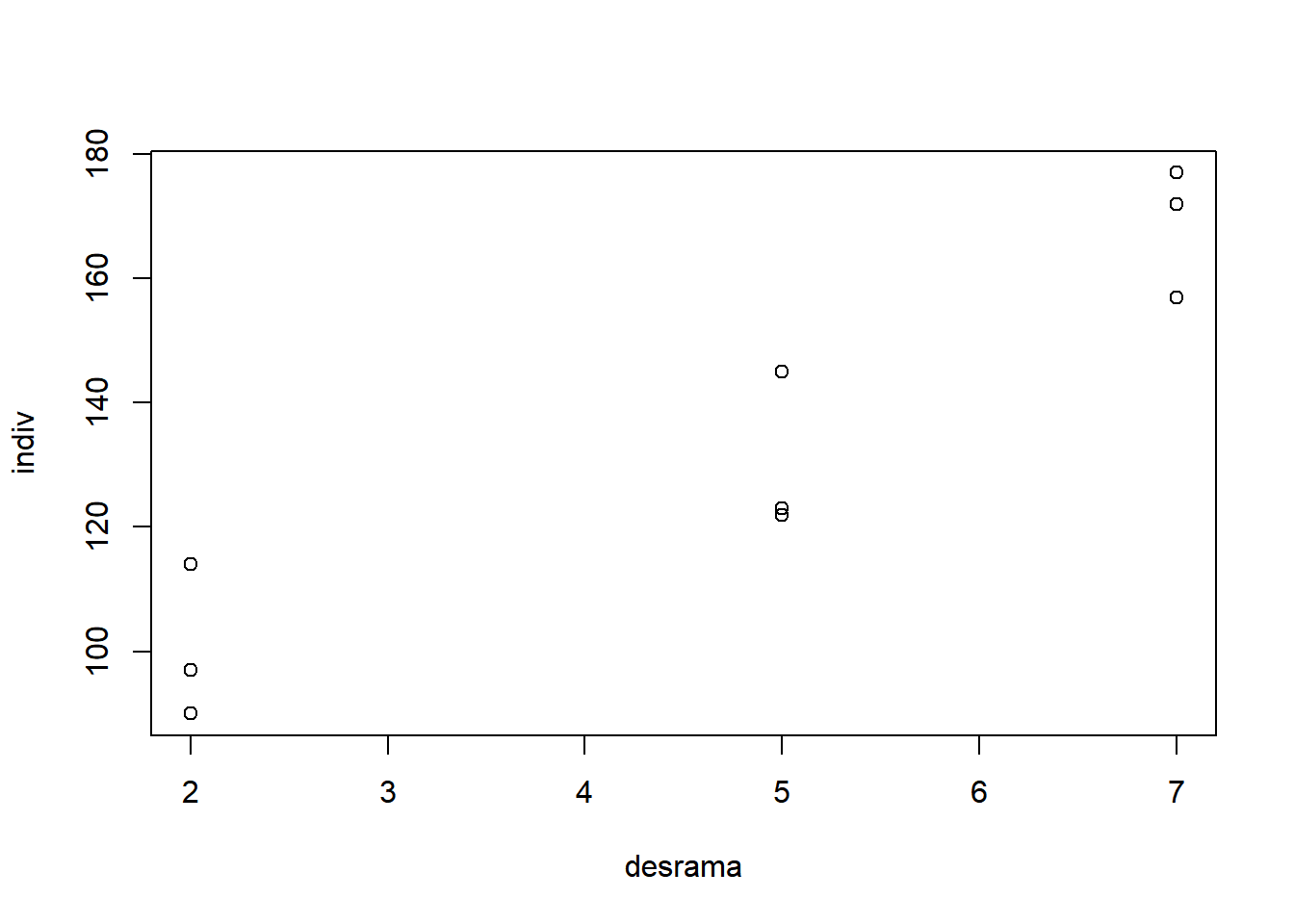
plot(data = sub[sub$floresta == "A",], indiv ~ desrama)

Fixando floresta igual a B:

plot(data = sub[sub$floresta == "B",], indiv ~ desrama)

Fixando floresta igual a C:

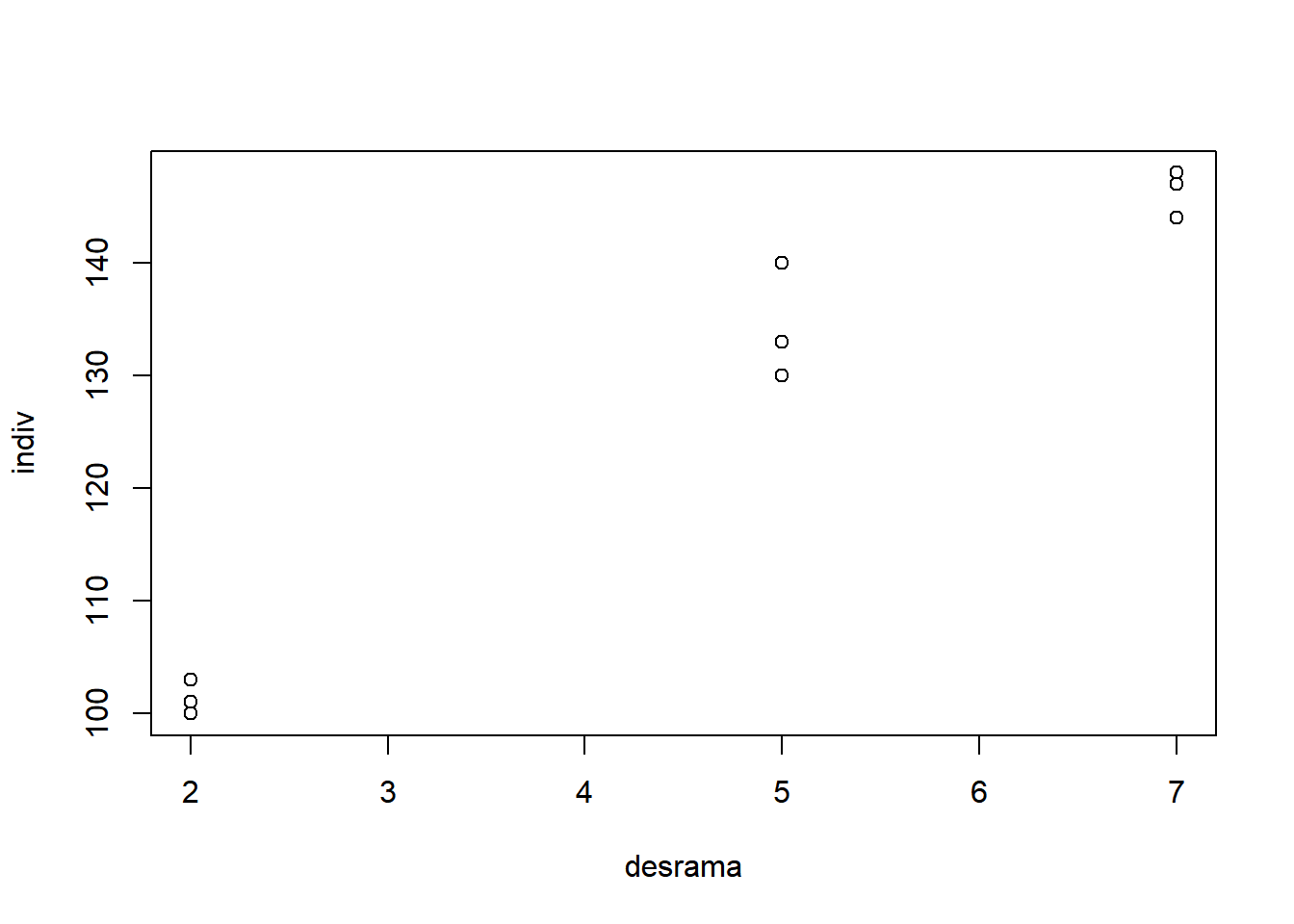
plot(data = sub[sub$floresta == "C",], indiv ~ desrama)

Analisando os gráficos acima, os fatores parecem significativos, assim como a interação. Quando o interesse é verificar a questão das pressuposições considerando os tratamentos (Parcela e Subparcela juntos), além das colunas referentes a parcela e subparcela, teria que ser acrescentado uma coluna para tratamentos. Ou seja, é como se fosse uma análise preliminar como DIC ou DBC.

O pacote ExpDes.pt não inclui as análises de pressuposições para o delineamento de parcelas subdivididas. Existem várias maneiras de contornar esta questão, uma delas é combinar as qualidades de diferentes pacotes. Aqui por exemplo, utiliza-se os testes estatísticos das pressuposições de um pacote e a ANOVA e desdobramentos do outro.

require(easyanova)
r.aov = ea2(sub, design=4)

Como já foi visto, o teste de normalidade e de homogeneidade podem ser obtidos na posição 10 da função ea2() do pacote easyanova.

r.aov[10]

## $`Residual analysis`
## $`Residual analysis`$values
##                                           values
## p.value Shapiro-Wilk test                 0.4583
## p.value Bartlett test (plot)              0.0036
## p.value Bartlett test (split.plot)        0.5945
## p.value Bartlett test (plot*split.plot)   0.0264
## AIC                                     171.9126
## BIC                                     182.5971
## first value most discrepant              14.0000
## second value most discrepant             12.0000
## third value most discrepant              17.0000
## Mean Square of Error a                   35.6667
## Mean Square of Error b                   64.0009
## Coefficient of Variation a                5.3589
## Coefficient of Variation b                7.1785
## 
## $`Residual analysis`$residuals
##           1           2           3           4 
##   0.6605916  -0.3252332  -0.3353584  10.3272582 
##           5           6           7           8 
##  -6.6585666  -3.6686917  -5.0060751  -0.9918999 
##           9          10          11          12 
##   5.9979750 -10.3191581  -3.3333333  13.6524915 
##          13          14          15          16 
##  -6.9858248  15.0000000  -8.0141752   3.3475085 
##          17          18          19          20 
## -11.6666667   8.3191581  -1.3252332  -0.3323208 
##          21          22          23          24 
##   1.6575540  -4.3252332  -1.3323208   5.6575540 
##          25          26          27 
##  -2.3252332   0.6676792   1.6575540 
## attr(,"label")
## [1] "Residuals"
## 
## $`Residual analysis`$`standardized residuals`
##           1           2           3           4 
##  0.09926874 -0.04887361 -0.05039514  1.55190283 
##           5           6           7           8 
## -1.00059939 -0.55130344 -0.75227538 -0.14905527 
##           9          10          11          12 
##  0.90133065 -1.55068561 -0.50090831  2.05159391 
##          13          14          15          16 
## -1.04977730  2.25408738 -1.20431008  0.50303845 
##          17          18          19          20 
## -1.75317907  1.25014062 -0.19914610 -0.04993868 
##          21          22          23          24 
##  0.24908478 -0.64996357 -0.20021117  0.85017474 
##          25          26          27 
## -0.34941859  0.10033381  0.24908478

Uma vez confirmadas as pressuposições, retorna-se ao pacote ExpDes.pt. A sintaxe da função para análise de parcela subdividida no pacote é:

psub2.dic(fator1, fator2, repet, resp, quali = c(TRUE, TRUE),
          mcomp = "tukey", fac.names = c("F1", "F2"), 
          sigT = 0.05, sigF = 0.05)

No exemplo tem-se o fator principal (fator 1) como qualitativo e o fator secundário (fator 2) como quantitativo. Assim informando os parâmetros obrigatórios juntamente com os parâmetros quali e fac.names (nomes dos fatores) tem-se:

require(ExpDes.pt)
psub2.dic(sub$floresta, sub$desrama, sub$rep, sub$indiv,
          quali = c(TRUE, FALSE), 
          fac.names = c("Floresta", "Desrama"))

## ------------------------------------------------------------------------
## Legenda:
## FATOR 1    (parcela):  Floresta 
## FATOR 2 (subparcela):  Desrama 
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## $`Quadro da analise de variancia`
##                  GL    SQ     QM      Fc Pr(>Fc)    
## Floresta          2 19073 9536.3 267.374   1e-06 ***
## Erro a            6   214   35.7                    
## Desrama           2 14795 7397.3  94.568 < 2e-16 ***
## Floresta*Desrama  4   799  199.7   2.553 0.09349 .  
## Erro b           12   939   78.2                    
## Total            26 35819                           
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## ------------------------------------------------------------------------
## CV 1 = 5.358865 %
## CV 2 = 7.936091 %
## 
## ------------------------------------------------------------------------
## #Teste de normalidade dos residuos (Shapiro-Wilk)
## valor-p:  0.5769146 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## Interacao nao significativa: analisando os efeitos simples
## ------------------------------------------------------------------------
## Floresta
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a     B   133 
## a     C   127.3333 
##  b    A   74 
## ------------------------------------------------------------------------
## 
## Desrama
## Ajuste de modelos polinomiais de regressao
## ------------------------------------------------------------------------
## 
## Modelo Linear
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  58.7193     4.2238    13.9021    0   
## b1  11.2982     0.8284    13.6395    0   
## -----------------------------------------
## 
## R2 do modelo linear
## --------
## 0.983607
## --------
## 
## Analise de variancia do modelo linear
## ==============================================================
##                      GL     SQ          QM        Fc   valor.p
## --------------------------------------------------------------
## Efeito linear        1  14,552.1400 14,552.1400 186.04    0   
## Desvios de Regressao 1   242.5263    242.5263    3.1   0.10371
## Residuos             12  938.6667     78.2222                 
## --------------------------------------------------------------
## ------------------------------------------------------------------------
## 
## Modelo quadratico
## ========================================
##    Estimativa Erro.padrao   tc   valor.p
## ----------------------------------------
## b0     75       10.1652   7.3781 0.00001
## b1   1.8667     5.4200    0.3444 0.7365 
## b2   1.0667     0.6058    1.7608 0.1037 
## ----------------------------------------
## 
## R2 do modelo quadratico
## -
## 1
## -
## 
## Analise de variancia do modelo quadratico
## ==============================================================
##                      GL     SQ          QM        Fc   valor.p
## --------------------------------------------------------------
## Efeito linear        1  14,552.1400 14,552.1400 186.04    0   
## Efeito quadratico    1   242.5263    242.5263    3.1   0.10371
## Desvios de Regressao 0       0           0        0       1   
## Residuos             12  938.6667     78.2222                 
## --------------------------------------------------------------
## ------------------------------------------------------------------------

Como esperado, foi observado a significância dos fatores: floresta e desrama. No entanto, a interação não foi significativa a 5%. Desta forma, não é necessário analisar a interação entre os fatores.

10.2 O caso desbalanceado

Neste exemplo desbalanceado será analisado um experimento em que três alturas de desrama são subdivididos em três espécies florestais. O efeito dos tratamentos foi medido através da produção de madeira em metros cúbicos.

Fator na parcela: Espécie florestal: A, B ou C.
Fator nas subparcelas: Desrama 2, 5 e 7 metros.
3 repetições.
Observações perdidas: Espécie A, desrama 2 metros e repetição 2. Espécie C, desrama 2 metros e repetição 2. Espécie C, desrama 5 metros e repetição 1. Espécie C, desrama 7 metros e repetição 1.
Variável de interesse: número de indivíduos regenerantes.

Table 10.2: Dados de outro experimento em parcela subdividida, porém desbalanceado.
especie	rep	desrama	volume
A	1	2	48
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	131
A	2	7	65
A	3	7	112
B	1	2	80
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	3	2	103
C	2	5	133
C	3	5	104
C	2	7	147
C	3	7	119

O primeiro passo é importar o arquivo contendo os resultados do experimento para dentro do R. Esta tarefa pode ser realizada através do seguinte comando:

sub2 = read.csv("./data/Experimento Subdividida 2.csv", sep = ",", dec = ".")

Os dados devem ser explorados graficamente antes de seguir com a análise de variância do experimento.

Considerando apenas tratamento principal:

boxplot(data = sub2, volume ~ especie)

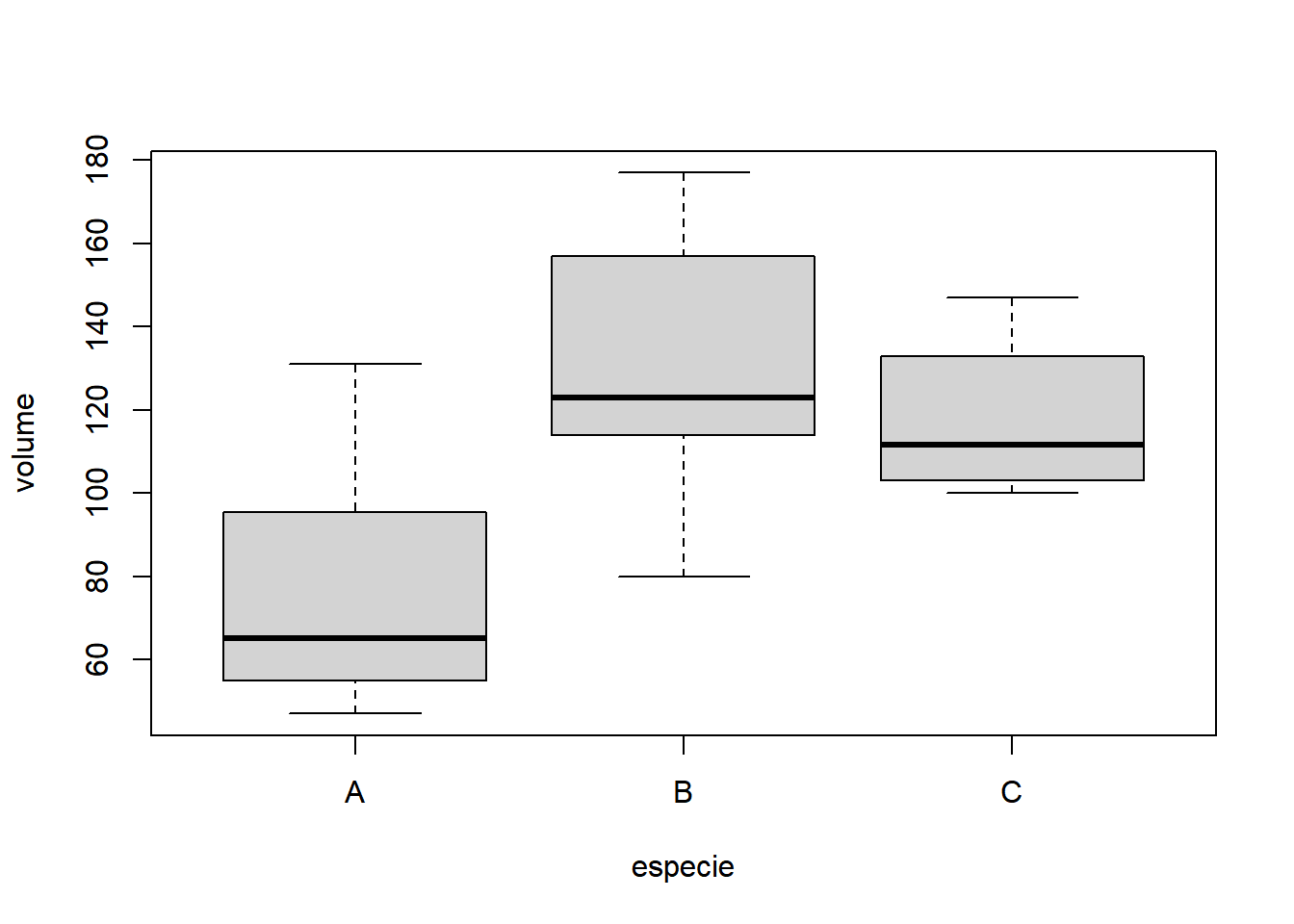
Considerando apenas tratamento secundário:

plot(data = sub2, volume ~ desrama)

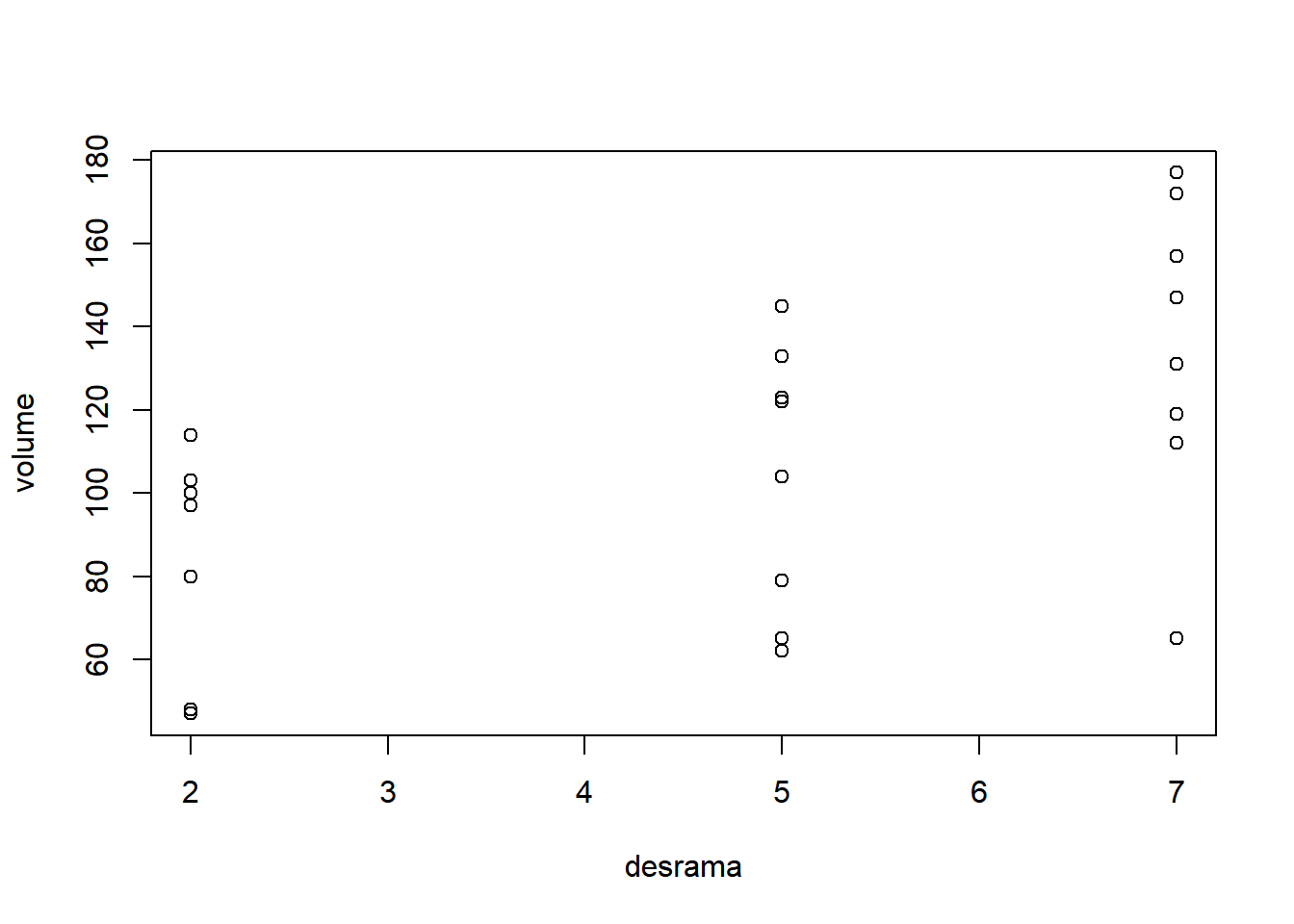
Interação dos tratamentos:

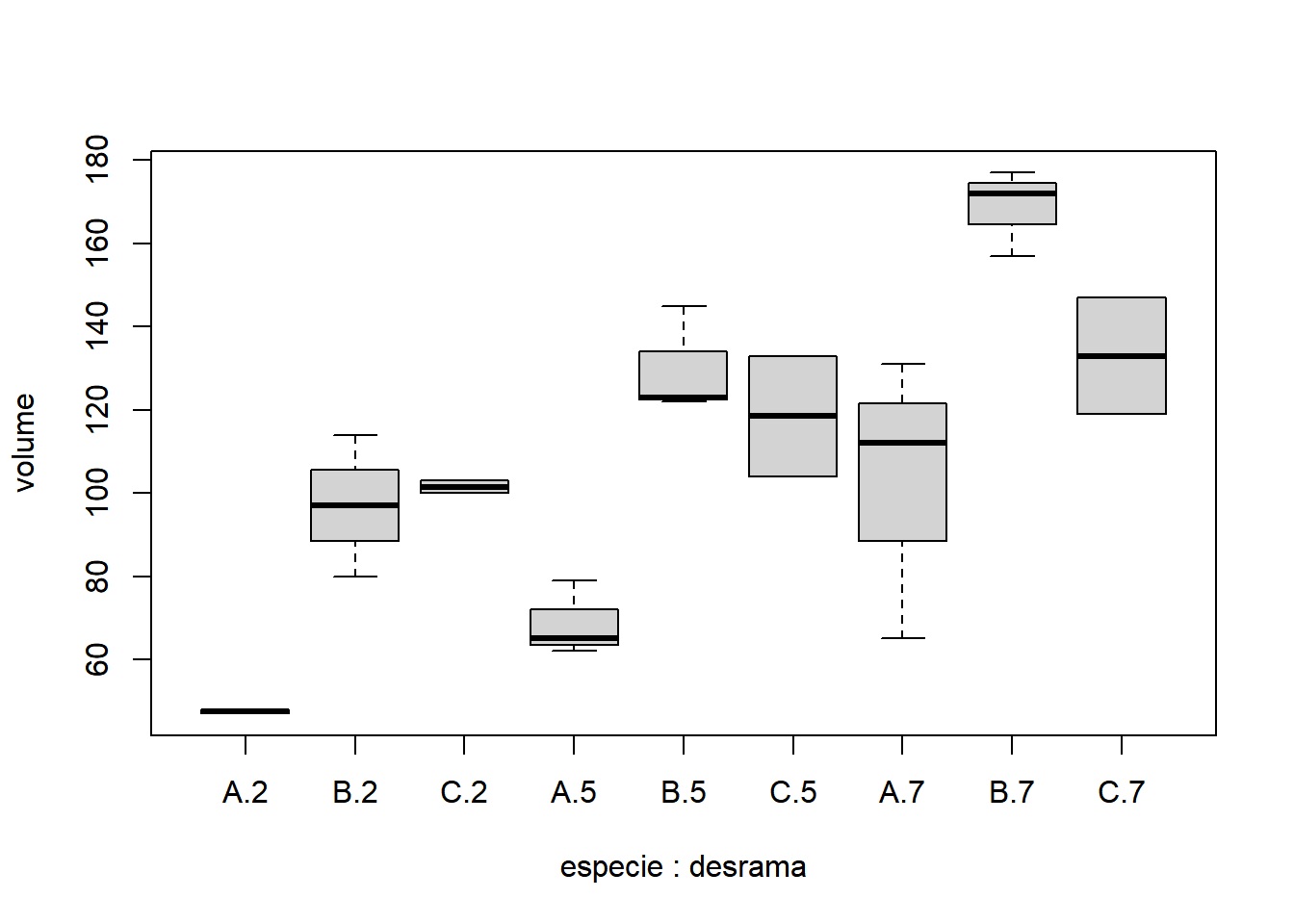
boxplot(data = sub2, volume ~ especie/desrama)

Fixando desrana até 2 metros:

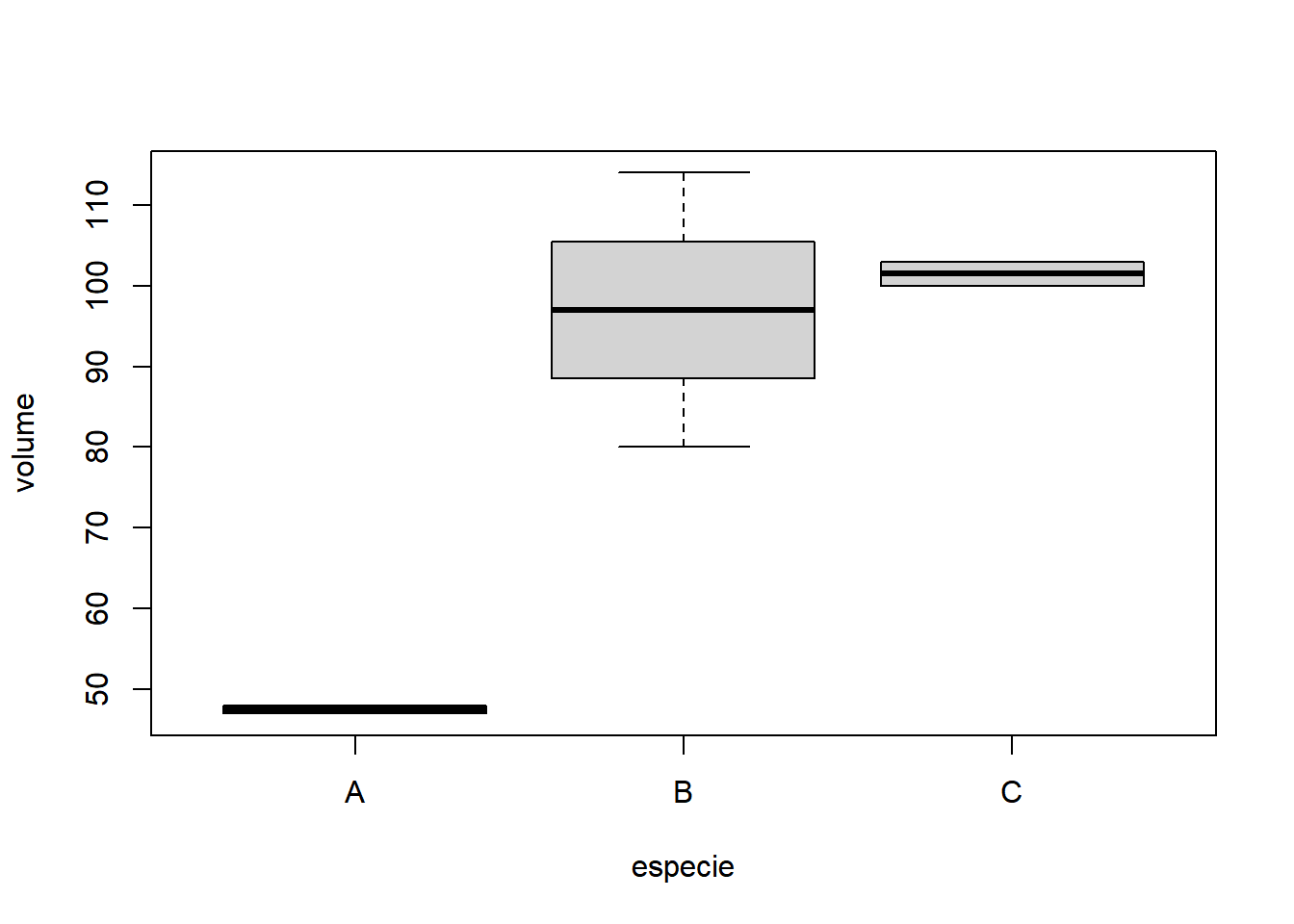
boxplot(data = sub2[sub2$desrama == 2,], volume ~ especie)

Fixando desrama até 5 metros:

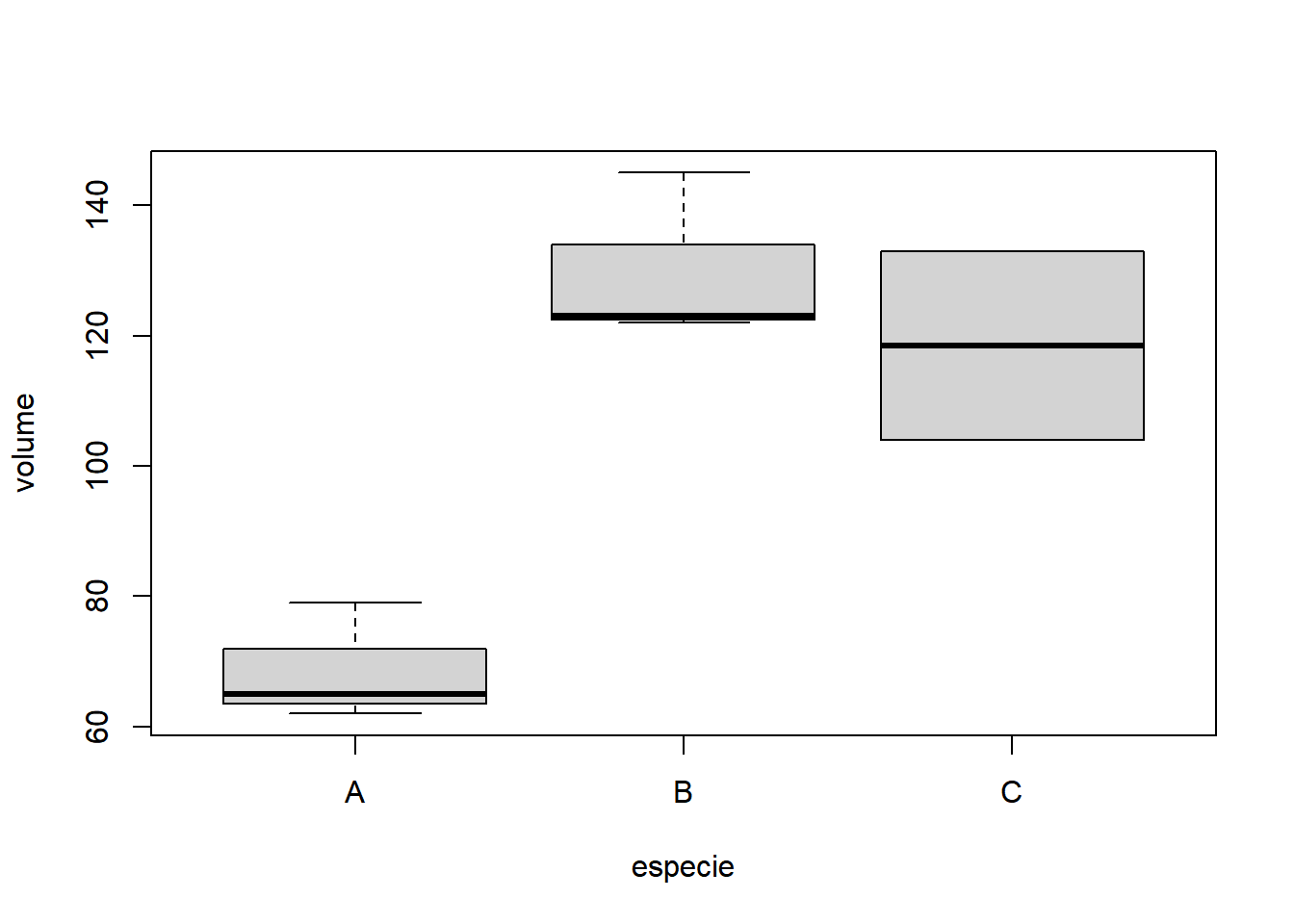
boxplot(data = sub2[sub2$desrama == 5,], volume ~ especie)

Fixando desrama até 7 metros:

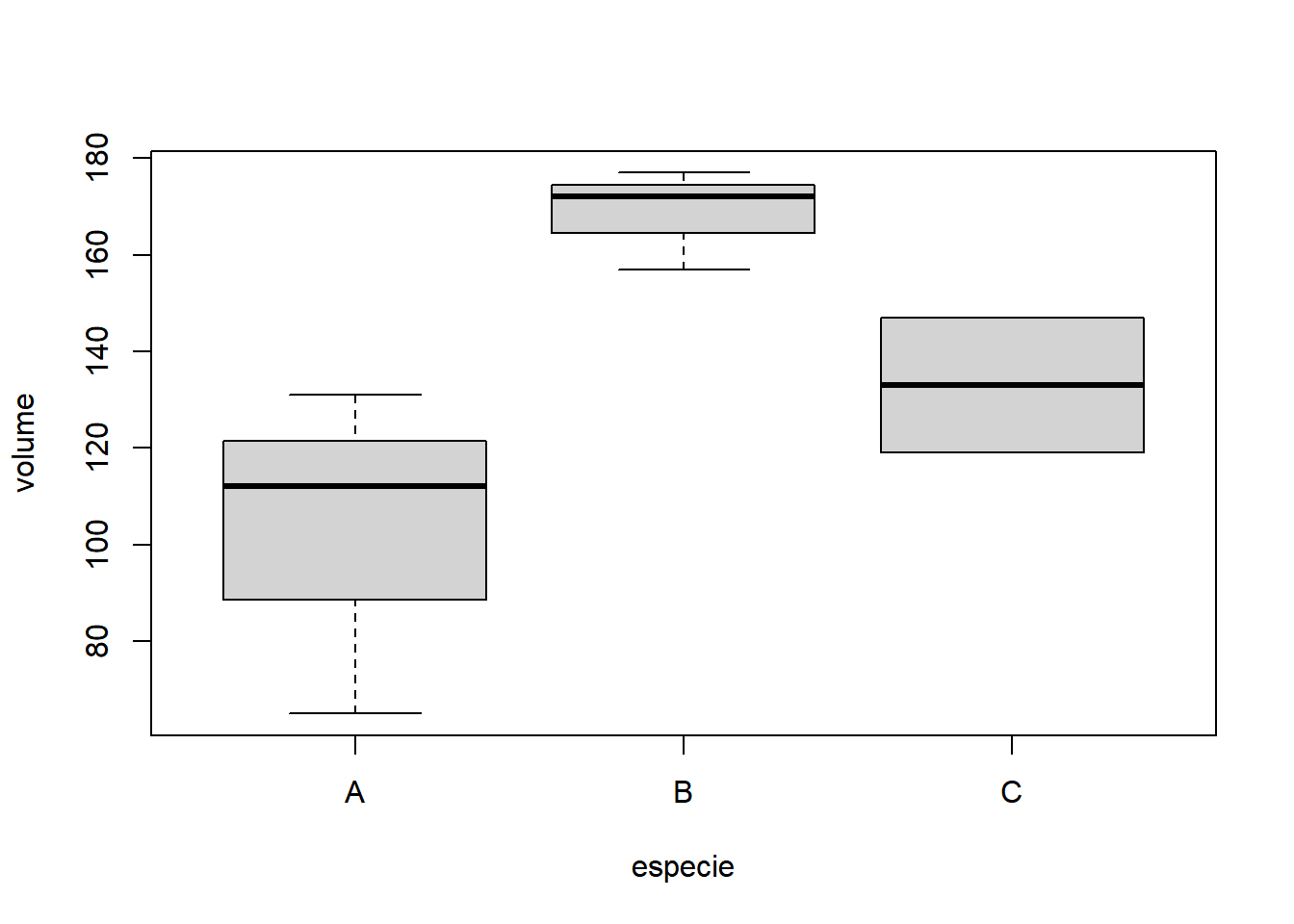
boxplot(data = sub2[sub2$desrama == 7,], volume ~ especie)

Fixando espécie igual a A:

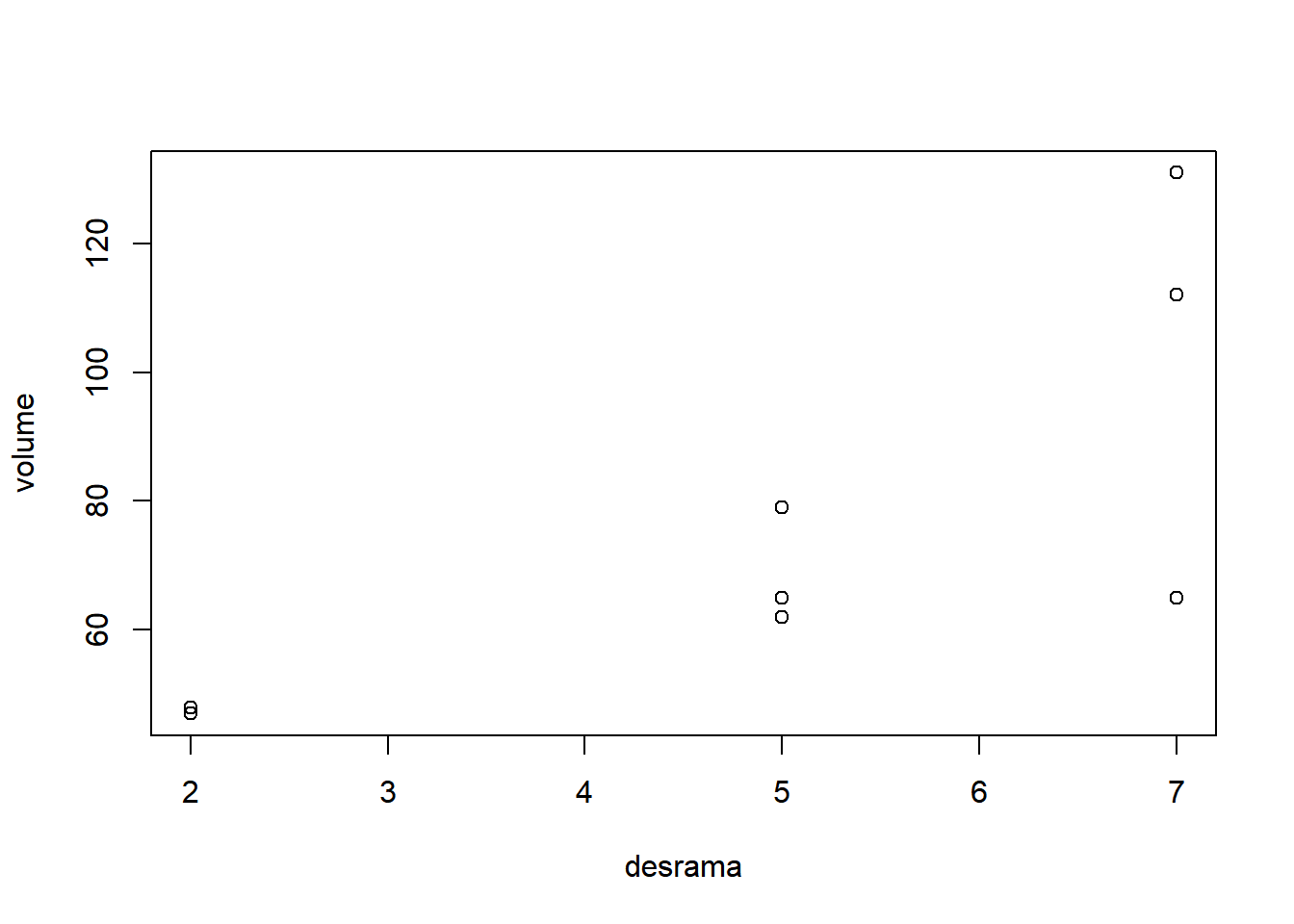
plot(data = sub2[sub2$especie == "A",], volume ~ desrama)

Fixando espécie igual a B:

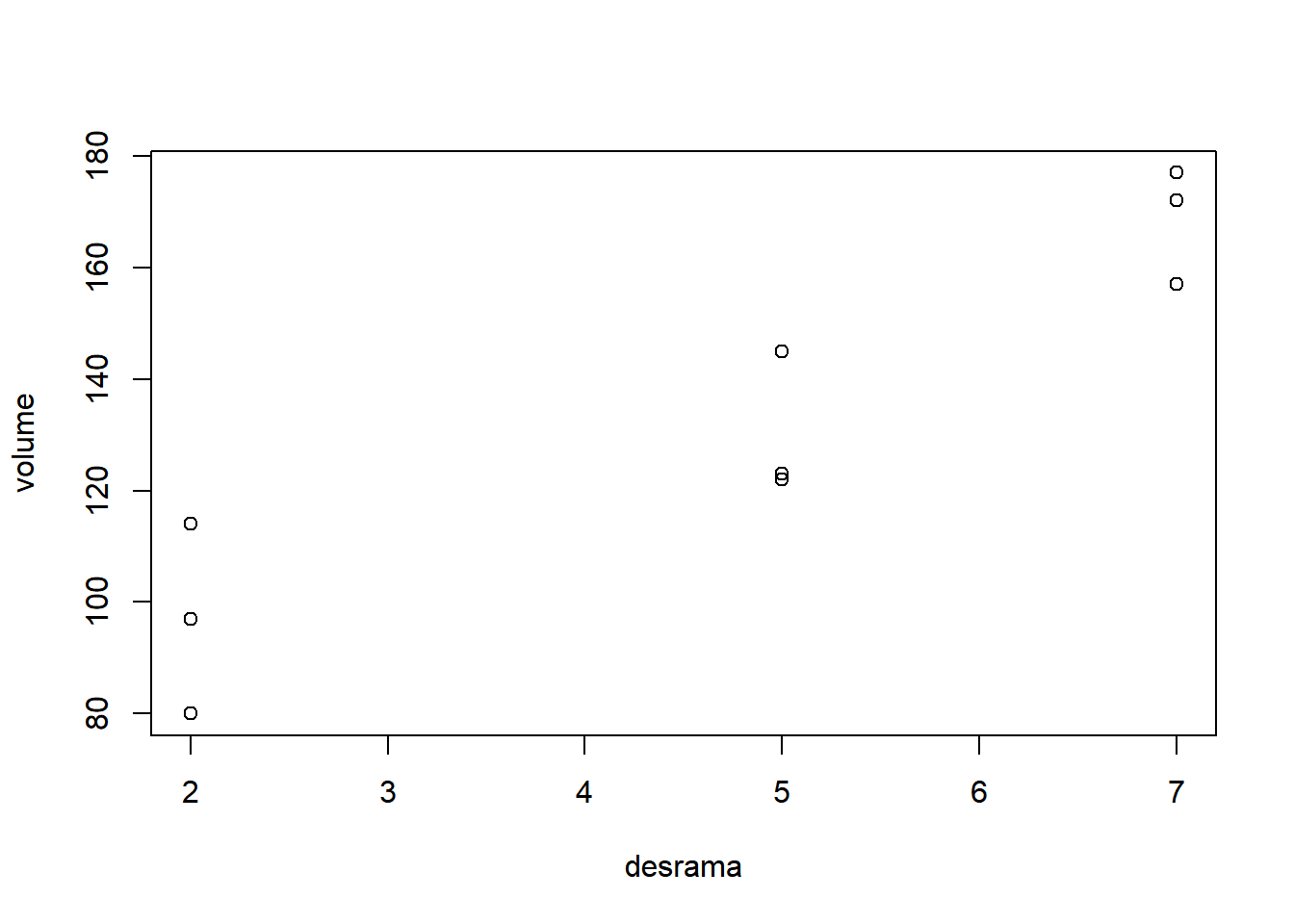
plot(data = sub2[sub2$especie == "B",], volume ~ desrama)

Fixando espécie igual a C:

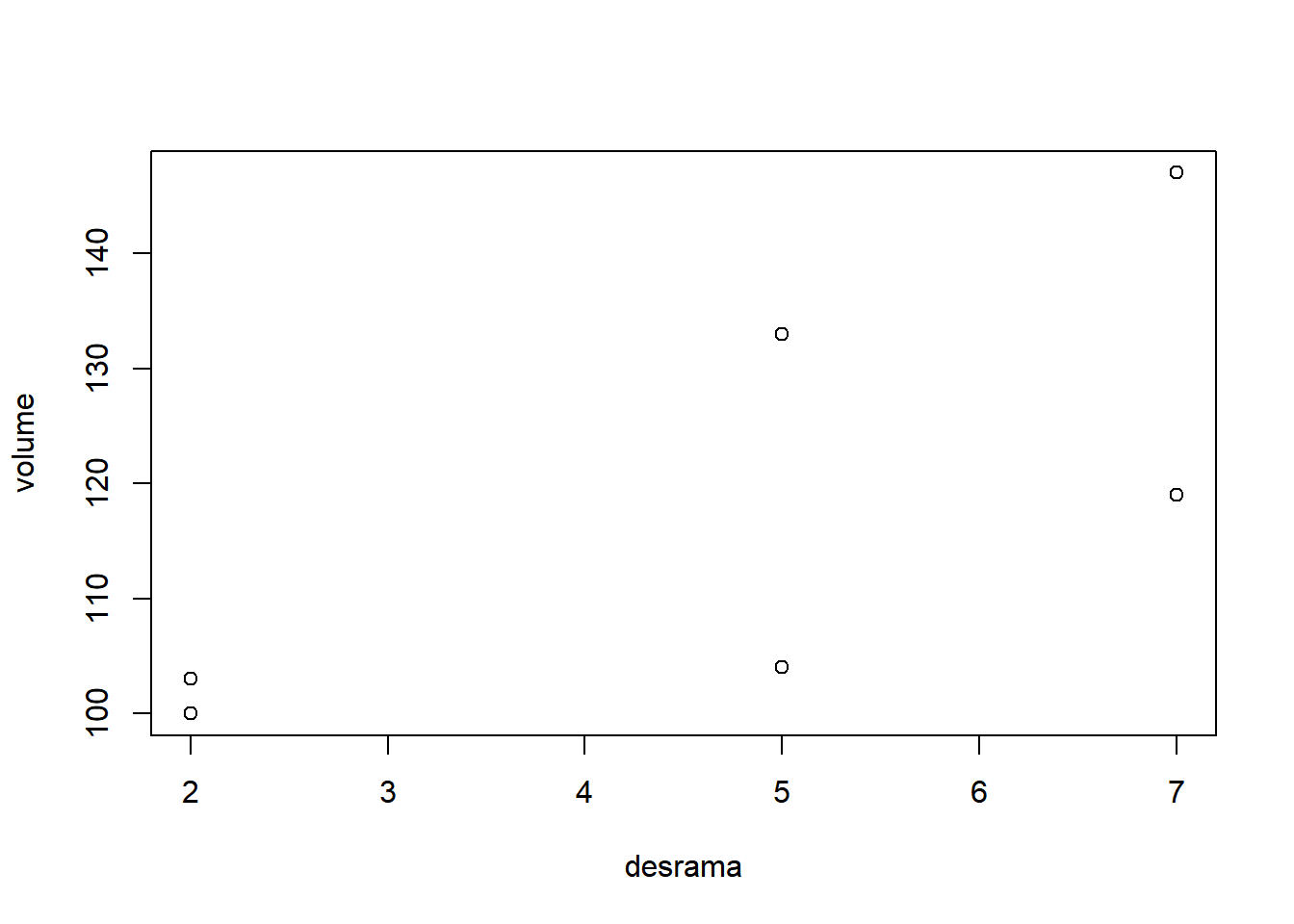
plot(data = sub2[sub2$especie == "C",], volume ~ desrama)

Os dados por se tratarem de experimento desbalanceados com efeito da interação relevante devem ser analisados com o pacote easyanova. A função será ea2() e possui a sintaxe básica:

ea2(data, design = 1, alpha = 0.05, cov = 4, list = FALSE, 
    p.adjust=1, plot=2)

Os dados devem ser apresentados na ordem:

Fator nas parcelas
Repetição
Fator nas subparcelas
Variável resposta

O parâmetro design deve ser definido como 4, resultando no seguinte comando:

require(easyanova)
r.aov = ea2(sub2, design=4)

Os resultados podem ser acessados escolhendo um dos elementos da lista:

r.aov[10]

## $`Residual analysis`
## $`Residual analysis`$values
##                                           values
## p.value Shapiro-Wilk test                 0.8313
## p.value Bartlett test (plot)              0.4160
## p.value Bartlett test (split.plot)        0.2427
## p.value Bartlett test (plot*split.plot)   0.6827
## AIC                                     165.0415
## BIC                                     172.7102
## first value most discrepant               7.0000
## second value most discrepant              6.0000
## third value most discrepant              13.0000
## Mean Square of Error a                  402.7662
## Mean Square of Error b                  220.3501
## Coefficient of Variation a               18.4488
## Coefficient of Variation b               13.6457
## 
## $`Residual analysis`$residuals
##           1           2           3           4 
##  -2.8241221   2.8241221   1.6212788   4.1091983 
##           5           6           7           8 
##  -5.7304770  19.6212788 -26.8908017   7.2695230 
##           9          10          11          12 
## -12.9589104  -0.6517886  13.6106990  -2.9589104 
##          13          14          15          16 
##  14.3482114 -11.3893010   7.3744229 -12.3184553 
##          17          18          19          20 
##   4.9440324  -3.5066019   3.5066019   7.9988237 
##          21          22          23 
##  -7.9988237   7.4988237  -7.4988237 
## attr(,"label")
## [1] "Residuals"
## 
## $`Residual analysis`$`standardized residuals`
##           1           2           3           4 
## -0.26911379  0.26911379  0.15449349  0.39157015 
##           5           6           7           8 
## -0.54606364  1.86973386 -2.56245492  0.69272107 
##           9          10          11          12 
## -1.23486923 -0.06210968  1.29697891 -0.28195792 
##          13          14          15          16 
##  1.36725729 -1.08529938  0.70271711 -1.17383954 
##          17          18          19          20 
##  0.47112244 -0.33414806  0.33414806  0.76221696 
##          21          22          23 
## -0.76221696  0.71457139 -0.71457139

O teste de normalidade apresentou valor não significativo, indicando assim que não há evidências para rejeitar a normalidade dos resíduos.

r.aov[1]

## $`Marginal anova (Type III Sum of Squares)`
##                 numDF denDF  F-value p-value
## plot                2     6 16.07861  0.0039
## split.plot          2     8 21.60633  0.0006
## plot:split.plot     4     8  1.27547  0.3555

Sendo a interação não significativa, os fatores (da parcela e da subparcela) devem ser analisados de forma independente.

Comparação das parcelas:

r.aov[2]

## $`Adjusted means (plot)`
##   plot adjusted.mean standard.error tukey snk duncan t
## 1    B      131.8889         7.6958     a   a      a a
## 2    C      118.3355         8.6638     a   a      a a
## 3    A       71.1485         8.0186     b   b      b b

Comparação das subdivisões:

r.aov[4]

## $`Adjusted means (split.plot)`
##   split.plot adjusted.mean standard.error tukey snk duncan
## 1          7      134.5013         6.4491     a   a      a
## 2          5      105.4458         6.4491     b   b      b
## 3          2       81.4258         6.8129     c   c      c
##   t
## 1 a
## 2 b
## 3 c

floresta	rep	desrama	indiv
A	1	2	48
A	2	2	47
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	101
A	2	7	105
A	3	7	112
B	1	2	90
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	2	2	101
C	3	2	103
C	1	5	130
C	2	5	133
C	3	5	140
C	1	7	144
C	2	7	147
C	3	7	148

especie	rep	desrama	volume
A	1	2	48
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	131
A	2	7	65
A	3	7	112
B	1	2	80
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	3	2	103
C	2	5	133
C	3	5	104
C	2	7	147
C	3	7	119

floresta	rep	desrama	indiv
A	1	2	48
A	2	2	47
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	101
A	2	7	105
A	3	7	112
B	1	2	90
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	2	2	101
C	3	2	103
C	1	5	130
C	2	5	133
C	3	5	140
C	1	7	144
C	2	7	147
C	3	7	148

especie	rep	desrama	volume
A	1	2	48
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	131
A	2	7	65
A	3	7	112
B	1	2	80
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	3	2	103
C	2	5	133
C	3	5	104
C	2	7	147
C	3	7	119

floresta	rep	desrama	indiv
A	1	2	48
A	2	2	47
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	101
A	2	7	105
A	3	7	112
B	1	2	90
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	2	2	101
C	3	2	103
C	1	5	130
C	2	5	133
C	3	5	140
C	1	7	144
C	2	7	147
C	3	7	148

especie	rep	desrama	volume
A	1	2	48
A	3	2	47
A	1	5	79
A	2	5	62
A	3	5	65
A	1	7	131
A	2	7	65
A	3	7	112
B	1	2	80
B	2	2	97
B	3	2	114
B	1	5	123
B	2	5	145
B	3	5	122
B	1	7	172
B	2	7	157
B	3	7	177
C	1	2	100
C	3	2	103
C	2	5	133
C	3	5	104
C	2	7	147
C	3	7	119