Cap. 2 Delineamentos experimentais

Delineamento experimental se trata do desenho do experimento. Ou seja, ele define a organização das unidades experimentais em função da pergunta científica que se deseja responder. Com base no delineamento escolhido, regras precisam ser seguidas, especialmente relacionados à maneira que os tratamentos são distribuídos nas unidades experimentais.

A unidade experimental é o objeto que identifica um sistema de interesse de uma pesquisa e representa uma unidade da população. É sobre a unidade experimental que os tratamento serão aplicados e avaliados.

Os tratamentos são variáveis manipuladas e controladas pelo pesquisador. Desta forma, qualquer outra influência tem que ocorrer ao acaso, e por isto, as unidades experimentais devem ser o homogêneas e o tratamento deve ser a ela atribuída de forma aleatória.

Outro ponto importante num delineamento experimental, é o número de repetições. Desta forma, deve haver unidades experimentais suficientes para que os tratamentos sejam aplicados e repetidos. Quanto maior o número de repetições, menor o intervalo de confiança e, portanto, mais precisa as inferências estatísticas. Existem metodologias específicas para a determinação do número ideal de repetições, mas na prática, adotam-se trabalhos anteriores como referência, ou mesmo a disponibilidade de material acaba definindo o número de repetições.

2.1 ANOVA

A Análise de Variância, ou simplesmente ANOVA, é uma análise estatística para determinar a contribuição de diferentes fatores na variância total de um experimento.

O método foi desenvolvido em 1925 por Ronald Fisher para experimentos balanceados, ou seja, experimentos com o mesmo número de repetições em cada tratamento. No entanto, correções foram desenvolvidas para tratar experimentos desbalanceados, como será observado mais adiante. Assim, podemos definir Análise de Variância (ANOVA) como uma técnica que decompõe a variância total e seus graus de liberdade em partes atribuídas a fatores controlados (tratamento) e a uma outra parte associada a uma causa não controlada, também chamada de resíduo.

2.1.1 Partição da variação

Suponha que estamos analisando o efeito de três materiais genéticos através de um experimento inteiramente casualizado. Cada tratamento foi formado por seis repetições, e cada repetição contendo 36 plantas. Tratamentos com a mesma quantidade de repetições formam um experimento balanceado. Resumindo:

Um fator com 3 tratamentos (i variando de 1 a 3)
6 repetições por tratamento (j variando de 1 a 6)
18 unidades experimentais presentes no experimento

A variável de interesse é a altura. Portanto, deseja observar se os tratamentos influenciam a altura das plantas. A média das alturas das árvores de cada uma das repetições é:

## Warning: package 'knitr' was built under R version 4.0.3

Table 2.1: Dados de exemplo.
Repeticao	MatGen1	MatGen2	MatGen3
Rep 1	21	19	18
Rep 2	20	19	18
Rep 3	20	17	15
Rep 4	17	13	13
Rep 5	18	16	13
Rep 6	17	14	13

Para analisar o experimento, será necessario obter a média e a soma para cada tratamento:

## Warning in read.table(file = file, header = header, sep
## = sep, quote = quote, : incomplete final line found by
## readTableHeader on './data/anova_sumRep.csv'

Table 2.2: Média e soma de cada tratamento.
Estatistica	MatGen1	MatGen2	MatGen3
Soma	?	?	?
Media	?	?	?

E também a soma e média geral:

## Warning in read.table(file = file, header = header, sep
## = sep, quote = quote, : incomplete final line found by
## readTableHeader on './data/anova_sumTotal.csv'

Table 2.3: Média e soma total.
Estatistica	Valor
Total geral	?
Media Geral	?

Todas as somas - sum() e médias - mean() que faltam nas tabelas acimas serão computadas uma a uma por meio de linhas de comando no R. Desta forma, aproveite para relembrar um pouco da sintaxe, bem como dos operadores matemáticos:

Entrar com os vetores correspondentes a cada tratamento com os valore de suas respectivas repetições.

matGen1 = c(21, 20, 20, 17, 18, 17)
matGen2 = c(19, 19, 17, 13, 16, 14)
matGen3 = c(18, 18, 15, 13, 13, 13)

Calcular a soma das repetições do tratamento 1.

s1 = sum(matGen1)
print (paste("Soma MATGEN1 = ", s1, sep = " "))

## [1] "Soma MATGEN1 =  113"

Calcular a média das repetições do tratamento 1.

m1 = mean(matGen1)
print (paste("Media MATGEN1 = ", m1, sep = " "))

## [1] "Media MATGEN1 =  18.8333333333333"

Calcular a soma das repetições do tratamento 2.

s2 = sum(matGen2)
print (paste("Soma MATGEN2 = ", s2, sep = " "))

## [1] "Soma MATGEN2 =  98"

Calcular a média das repetições do tratamento 2.

m2 = mean(matGen2)
print (paste("Media MATGEN1 = ", m2, sep = " "))

## [1] "Media MATGEN1 =  16.3333333333333"

Calcular a soma das repetições do tratamento 3.

s3 = sum(matGen3)
print (paste("Soma MATGEN3 = ", s3, sep = " "))

## [1] "Soma MATGEN3 =  90"

Calcular a média das repetições do tratamento 3.

m3 = mean(matGen3)
print (paste("Media MATGEN3 = ", m3, sep = " "))

## [1] "Media MATGEN3 =  15"

Calcular a soma de todas as repetições, dos três tratamentos.

somaTotal = sum(c(matGen1, matGen2, matGen3))
print (paste("Soma total = ", somaTotal, sep = " "))

## [1] "Soma total =  301"

Calcular a média geral de todos os tratamentos e repetições.

mediaGeral = mean(c(matGen1, matGen2, matGen3))
print (paste("Media geral = ", mediaGeral, sep = " "))

## [1] "Media geral =  16.7222222222222"

A partir dos resultados obtidos nas etapas anteriores, as tabelas ficarão assim:

## Warning in read.table(file = file, header = header, sep
## = sep, quote = quote, : incomplete final line found by
## readTableHeader on './data/anova_sumRep2.csv'

Table 2.4: Média e soma de cada tratamento calculado.
Estatistica	MatGen1	MatGen2	MatGen3
Soma	113.00	98.00	90
Media	18.83	16.33	15

## Warning in read.table(file = file, header = header, sep
## = sep, quote = quote, : incomplete final line found by
## readTableHeader on './data/anova_sumTotal2.csv'

Table 2.5: Média e soma total calculado.
Estatistica	Valor
Total geral	301.00
Media Geral	16.72

2.1.1.1 Soma de quadrados total

O próximo passo é analisar a diferença de cada uma das 18 observações (3 tratamentos * 6 repetições cada) em relação à média geral:

\[desvio = x_{ij} - \bar{x}\]

em que j indica a repetição variando de 1 a 6; e i indica o tratamento variando de 1 a 3.

No R, esta operação fica fácil, pois é possível fazer de uma única vez a subtração dos elementos de um vetor pela média geral:

desvio1 = matGen1 - mediaGeral
desvio1

## [1] 4.2777778 3.2777778 3.2777778 0.2777778 1.2777778
## [6] 0.2777778

desvio2 = matGen2 - mediaGeral
desvio2

## [1]  2.2777778  2.2777778  0.2777778 -3.7222222 -0.7222222
## [6] -2.7222222

desvio3 = matGen3 - mediaGeral
desvio3

## [1]  1.277778  1.277778 -1.722222 -3.722222 -3.722222
## [6] -3.722222

Tabulando os desvios calculados acima, tem-se uma tabela da seguinte forma:

Table 2.6: Desvio da observação para e média geral.
MatGen1	MatGen2	MatGen3
4.28	2.28	1.28
3.28	2.28	1.28
3.28	0.28	1.72
0.28	-3.72	-3.72
1.28	-0.72	-3.72
0.28	-2.72	-3.72

Elevando cada um dos desvios ao quadrado e somando, obtem-se a soma de quadrados total (SQTotal). Esta soma de quadrados é a variação total dos dados.

\[SQTotal = \sum (x_{ij} - \bar{x})^2\]

em que i indica a repetição variando de 1 a 6 e j indica o tratamento variando de 1 a 3. A soma de quadrados total pode ser obtida com:

sqTotal = sum(desvio1^2, desvio2^2, desvio3^2)
print(sqTotal)

## [1] 121.6111

2.1.1.2 Soma de quadrados dos tratamentos

A soma de quadrados dos tratamentos, ou a soma de quadrados entre os tratamentos, pode ser calculada pela diferença entre a média de cada tratamento em relação à média geral.

\[desvio_{i} = \bar{x}_{i} - \bar{x}\]

em que j indica a repetição variando de 1 a 6 e i indica o tratamento variando de 1 a 3. Para isto, o valor de cada repetição é substituído pela média do seu tratamento. Isto é, através da fórmula rep, cria-se um vetor com a média do material genético repetida 6 vezes. Com esse procedimento, elimina-se o efeito do erro, já que cada tratamento será representado j vezes pelo valor da sua média. Finalmente, cada repetição é subtraída pela média geral.

desvioTrat1 = rep(mean(matGen1), 6) - mediaGeral
desvioTrat1

## [1] 2.111111 2.111111 2.111111 2.111111 2.111111 2.111111

desvioTrat2 = rep(mean(matGen2), 6) - mediaGeral
desvioTrat2

## [1] -0.3888889 -0.3888889 -0.3888889 -0.3888889 -0.3888889
## [6] -0.3888889

desvioTrat3 = rep(mean(matGen3), 6) - mediaGeral
desvioTrat3

## [1] -1.722222 -1.722222 -1.722222 -1.722222 -1.722222
## [6] -1.722222

Trazendo os resultados do R para uma tabela de desvios tem-se:

Table 2.7: Desvio entre a média do tratamento e média geral.
MatGen1	MatGen2	MatGen3
2.11	-0.39	-1.72
2.11	-0.39	-1.72
2.11	-0.39	-1.72
2.11	-0.39	-1.72
2.11	-0.39	-1.72
2.11	-0.39	-1.72

Os desvios são então elevados ao quadrado e somados, resultando na soma de quadrados dos tratamentos (SQTrat):

sqTrat = sum(desvioTrat1^2, desvioTrat2^2, desvioTrat3^2)
print(sqTrat)

## [1] 45.44444

2.1.1.3 Soma de quadrados dos resíduos

A soma de quadrados dos resíduos (SQRes) é também conhecida como soma de quadrados dentro do tratamento. Primeiro, calcula-se o desvio entre a cada uma das repetições e a média do respectivo tratamento:

\[desvio = x_{ij} - \bar{x}_{i}\] No R, podemos calcular da seguinte forma:

desvioRes1 = matGen1 - mean(matGen1)
desvioRes1

## [1]  2.1666667  1.1666667  1.1666667 -1.8333333 -0.8333333
## [6] -1.8333333

desvioRes2 = matGen2 - mean(matGen2)
desvioRes2

## [1]  2.6666667  2.6666667  0.6666667 -3.3333333 -0.3333333
## [6] -2.3333333

desvioRes3 = matGen3 - mean(matGen3)
desvioRes3

## [1]  3  3  0 -2 -2 -2

Trazendo os resultados do R para uma tabela de desvios tem-se:

Table 2.8: Desvio da observação para e média do tratamento
MatGen1	MatGen2	MatGen3
2.17	2.67	3
1.17	2.67	3
1.17	0.67	0
-1.83	-3.33	-2
0.83	0.33	-2
-1.83	-2.33	-2

Elevando cada desvio ao quadrado e somando-os, calcula-se a soma de quadrados dos resíduos:

sqRes = sum(desvioRes1^2, desvioRes2^2, desvioRes3^2)
print(sqRes)

## [1] 76.16667

2.1.1.4 Quadrado médio

O próximo passo é montar o quadro da ANOVA e determinar os quadrados médios:

## Warning in read.table(file = file, header = header, sep
## = sep, quote = quote, : incomplete final line found by
## readTableHeader on './data/anova_qm.csv'

Table 2.9: Fórmulas para o caluclo do quandrado médio.
Fonte.de.variacao	Soma.de.quadrados	Graus.de.liberdade	Quadrado.medio
Trat	SQTrat	\(i-1\)	\(SQTotal / (i-1)\)
Residuos	SQRes	\(i * (j - 1)\)	\(SQRes / (i * (j-1))\)
Total	SQTotal	\((i * j) - 1\)

Tanto a soma de quadrados, como os graus de liberdade são aditivos. Isto é, obtendo dois termos do quadro de variância, o terceiro pode ser obtido pela diferença.

Na prática, calcula-se a soma de quadrados total e a soma de quadrados do tratamento. Por diferença, obtém-se a soma de quadrados dos resíduos. O mesmo raciocínio vale para os graus de liberdade.

O quadrado médio, nada mais é que uma variância. Por isso, divide-se a soma de quadrados pelos graus de liberdade. Os quadrados médios são calculados da seguinte forma:

Quadrado médio dos tratamentos

qmTrat = sqTrat / (3 - 1)
print(qmTrat)

## [1] 22.72222

Quadrado médio do residuo

qmRes = sqRes / (3 * (6 - 1))
print(qmRes)

## [1] 5.077778

2.1.1.5 Teste F

Assim, o objetivo final da ANOVA é comparar a variância dos tratamentos relativa à variância dos resíduos. O valor da razão entre estas duas variâncias segue a distribuição F, recorrendo-se então à uma tabela de distribuição amostral da razão F para avaliar a significância do teste.

Fcalc = qmTrat / qmRes
print(Fcalc)

## [1] 4.474836

O quadro final da ANOVA será:

## Warning in read.table(file = file, header = header, sep
## = sep, quote = quote, : incomplete final line found by
## readTableHeader on './data/anova_final.csv'

Table 2.10: Quandro final da ANOVA
Fonte.de.variacao	Soma.de.quadrados	Graus.de.liberdade	Quadrado.medio	FCalc
Trat	45.44	2	22.72	4.47
ResÃduos	76.17	15	5.08	NA
Total	121.61	17	NA	NA

A hipótese nula é de que a variância entre os tratamentos é igual à variância populacional, ou variância dos resíduos. Um teste não significativo aceita-se a hipótese nula. Já um teste significativo rejeita-se a hipótese nula.

Ftabelado = qf(0.95, 2, 15)
print(Ftabelado)

## [1] 3.68232

Neste exercício, o F calculado é superior ao F tabelado. Assim o teste F é significativo e a hipótese nula é rejeitada para um nível de significância de 95%. A variância dos tratamentos não pode ser considerada igual à variância da população. Na prática isto indica que existe um efeito significativo dos tratamentos, e que pelo menor um dos tratamentos diferem dos demais.

Se o teste F é não significativo (F calculado < F tabelado), entende-se que os tratamentos não influenciaram as observações e a análise de seu experimento encerra-se aqui.

Por outro lado, o teste F significativo indica que pelo menos um dos tratamentos influenciou os dados observados. Se apenas dois tratamentos tiverem sido realizados, o teste F é conclusivo e as médias dos tratamentos podem ser comparadas diretamente. Se três ou mais tratamentos estiverem sendo comparados, o teste F é inconclusivo, uma vez que diz apenas que existe uma influência dos tratamentos, sem no entanto indicar qual deles é igual ou diferente. Assim uma pergunta surge: como os tratamentos se diferem uns dos outros?

Entram em cena os testes de médias ou a análise de regressão. Quando os tratamentos são qualitativos e significativos, o teste de médias irá dizer quais tratamentos são iguais e quais tratamentos são diferentes. Quando os tratamentos são quantitativos e significativos, utiliza-se a análise de regressão para definir o ponto ótimo. Dependendo do objetivo do experimento, mesmo tratamentos quantitativos podem ser analisados por meio de um teste de médias.

Para facilitar, a figura a seguir resume o que foi visto até agora por meio de uma árvore de decisão:

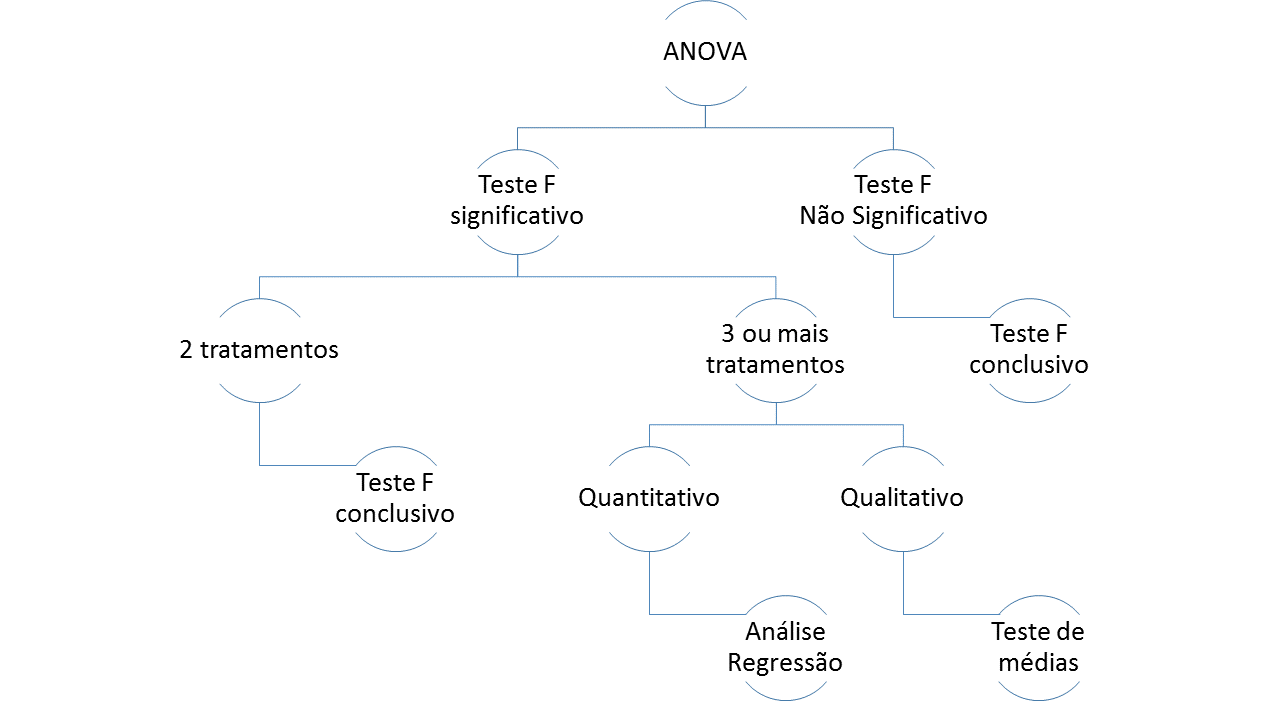
Fluxograma de decisão para interpretação de uma ANOVA

2.2 Tipos de ANOVA

Existem pelo menos 3 formas para se calcular a soma de quadrados da ANOVA, que são conhecidos como soma de quadrados do TIPO I, TIPO II e TIPO III. Esta notação foi introduzida pelo software SAS, mas acabou sendo adotada pela comunidade para diferenciar entre as diferentes formas de se calcular a soma de quadrados para composição da ANOVA.

A recomendação de uso dos diferentes tipos de soma de quadrados leva a calorosas discussões entre estatísticos. De modo geral, o tipo I é o padrão usado para dados balanceados. O tipo II e tipo III são mais indicados para dados desbalanceados. Quando o experimento é balanceado, os três tipos de ANOVA apresentam resultados idênticos.

2.2.1 Variações no cálculo da soma de quadrados

Partindo de um experimento que considere dois fatores A e B; sendo dois fatores principais e a interação AB, o modelo completo pode ser representado por SQ(A, B, AB). Também podem ser considerados modelos parciais como SQ(A, B) que indica um modelo sem interação, ou como SQ(B, AB) que indica um modelo que não considera efeitos do fator A.

A influência de um determinado fator (ou interação) é testada examinando as diferenças entre os modelos. Por exemplo, para determinar a presença de interação entre os fatores, um teste F é conduzido comparando o modelo com interação SQ(A, B, AB) e o modelo sem interação SQ(A, B).

2.2.2 ANOVA Tipo I

A ANOVA tipo I testa primeiro o efeito de A, seguido do efeito de B dado que se conhece A, seguido pela interação dado que os efeitos principais já são conhecidos. Esta ordem natural (A -> B -> AB) é a razão desta ANOVA ser conhecida como soma de quadrados sequencial.

SQ(A) para o fator A.
SQ(B | A) para fator B.
SQ(AB | B, A) para interação AB.

2.2.3 ANOVA Tipo II

Este tipo de ANOVA testa o efeito de um dos fatores principais dado que o outro já é conhecido. Assim, assume-se a não significância da interação.

Sugere-se no entanto que se teste SQ(AB | A, B). Se de fato a interação for não significativa, então o tipo II é estatisticamente mais poderoso que o tipo III.

SQ(A | B) para o fator A.
SQ(B | A) para o fator B.

2.2.4 ANOVA Tipo III

Este tipo de ANOVA só é válido quando a interação é significativa. No entanto, em muitos casos não se tem interesse em analisar os fatores principais quando a interação está presente, ou seja, na presença de interação, os efeitos principais deixam de ser interessantes isoladamente.

SQ(A | B, AB) para o fator A.
SQ(B | A, AB) para o fator B.

Assim, na prática, só é necessário preocupar com dados desbalanceados quando a interação entre fontes de variação for considerada no modelo estatístico do experimento.