Cap. 6 Delineamento inteiramente casualizado

Este é sem dúvida o caso mais simples dos delineamentos experimentais. Aqui, o fenômeno de estudo se resume a apenas duas fontes de variação: uma fonte de variação conhecida, determinada pelo tratamento e uma fonte de variação desconhecida, determinada pelo resíduo.

6.1 Recapitulando

A análise começa pela determinação das somas de quadrados total, que é formada pela soma de quadrados do tratamento e pela soma de quadrados do resíduo. Uma vez obtidas as somas de quadrados, calculam-se os quadrados médios e o valor da estatística F. Se F calculado for superior ao F tabelado, assume-se que existe um efeito devido aos tratamentos, ao passo que se F calculado for inferior ao F tabelado, não há evidências suficientes para rejeitar a hipótese nula, aceitando-se a hipótese de que não existe efeito dos tratamentos.

Sendo o efeito dos tratamentos significativo, realiza-se o desdobramento por meio de um teste de médias, se os tratamentos forem qualitativos, ou por meio de uma análise de regressão se os tratamentos forem quantitativos.

6.2 O caso balanceado

Para exemplificar o caso balanceado, será analisado um estudo sobre a influência de três diferentes tipos de substrato no crescimento em altura de mudas. Cada tipo de substrato foi utilizado na germinação de 10 plantas. 90 dias após o semeio, as alturas das plântulas foram medidas e registradas numa planilha eletrônica. Os dados podem ser assim resumidos:

Tratamento: 3 substratos
10 repetições
Variável de interesse: altura

Abaixo seguem as medições de altura tabuladas. Embora o R seja compatível com diversas extensões de planilhas eletrônicas, serão utilizados ao longo do livro arquivos em extensão .csv.

Table 6.1: Dados de delineamento inteiramente casualizado
tratamento	rep	altura
Substrato 1	1	1.2
Substrato 1	2	8.6
Substrato 1	3	8.6
Substrato 1	4	3.7
Substrato 1	5	9.9
Substrato 1	6	2.5
Substrato 1	7	6.2
Substrato 1	8	6.2
Substrato 1	9	1.2
Substrato 1	10	3.7
Substrato 2	1	2.5
Substrato 2	2	8.6
Substrato 2	3	7.4
Substrato 2	4	6.2
Substrato 2	5	9.9
Substrato 2	6	2.5
Substrato 2	7	6.2
Substrato 2	8	6.2
Substrato 2	9	1.2
Substrato 2	10	3.7
Substrato 3	1	3.7
Substrato 3	2	9.9
Substrato 3	3	11.1
Substrato 3	4	7.4
Substrato 3	5	7.4
Substrato 3	6	3.7
Substrato 3	7	6.2
Substrato 3	8	8.6
Substrato 3	9	11.1
Substrato 3	10	11.1

O primeiro passo é importar o arquivo csv contendo o experimento para dentro do R. Esta tarefa pode ser realizada através do seguinte comando:

dic1 = read.csv("./data/Experimento DIC 1.csv")

Com a importação, cria-se um objeto chamado dic1, contendo os dados do experimento num formato de dataframe.

Antes de partir para a análise, é fundamental explorar os dados de forma gráfica para conhecer melhor as relações e antecipar o resultado da análise estatística. A construção do gráfico ajuda na compreensão do fenômeno estudado e na validação da análise estatística escolhida. Por se tratar de um experimento com o tratamento formado por níveis qualitativos, recomenda-se o uso do boxplot().

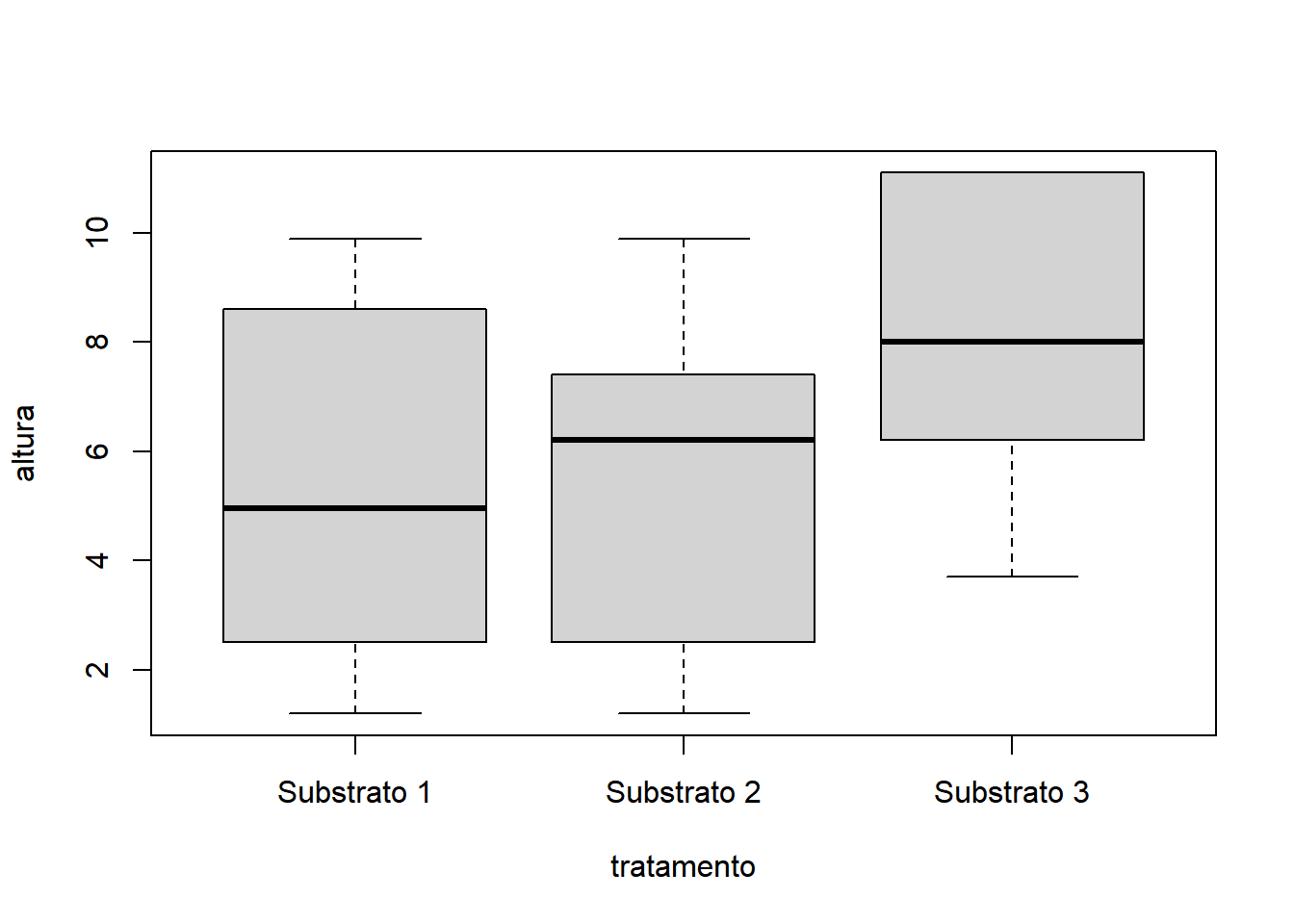
boxplot(data = dic1, altura ~ tratamento)

Pelo gráfico obtido, é razoável esperar que não haja diferenças significativas entre os tratamentos (3 substratos), pois existe uma grande sobreposição entre os interquartis dos substratos. Assim, espera-se que a análise estatística do experimento corrobore a conclusão empírica baseada no interpretação do gráfico.

Com a função dic() do pacote ExpDes.pt será possível realizar toda a análise de um experimento de delineamento inteiramente casualizado, inclusive o desdobramento caso o teste F seja significativo e o tratamento tenha três ou mais níveis.

Lembre-se que o pacote ExpDes.pt não faz parte da instalação padrão do R, e precisa ser adicionado à parte. A sintaxe básica da função dic() é:

dic(trat, resp, quali = TRUE, mcomp = "tukey", sigT = 0.05, sigF = 0.05)

Neste experimento, não será necessário alterar nenhum parâmetro opcional, sendo então o comando construído da seguinte maneira:

require(ExpDes.pt)
dic(dic1$tratamento, dic1$altura)

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL      SQ      QM     Fc    Pr>Fc
## Tratamento  2  49.299 24.6493 2.7908 0.079121
## Residuo    27 238.476  8.8324                
## Total      29 287.775                        
## ------------------------------------------------------------------------
## CV = 47.83 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos ( Shapiro-Wilk ) 
## Valor-p:  0.06889791 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia 
## valor-p:  0.937449 
## De acordo com o teste de bartlett a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
## 
## De acordo com o teste F, as medias nao podem ser consideradas diferentes.
## ------------------------------------------------------------------------
##        Niveis Medias
## 1 Substrato 1   5.18
## 2 Substrato 2   5.44
## 3 Substrato 3   8.02
## ------------------------------------------------------------------------

A primeira parte da análise é o quadro da variância que apresenta as fontes de variação com seus respectivos graus de liberdade, somas de quadrado e quadrados médio. Neste quadro também é apresentado o resultado do F calculado, que é a razão do quadrado médio do tratamento com o quadrado médio do resíduo.

No capítulo sobre a análise de variância, o quadro da ANOVA terminava com o F calculado, sendo seguido pela análise de uma tabela da estatística F para comparar o valor do F calculado com o valor de F tabelado. Nos softwares, não é necessário recorrer à tabela F, já que o p-valor oferece uma interpretação direta da significância.

O p-valor do experimento foi 0,079121, o que equivale à um grau de significância de 7,9%. Sendo o nível de significância do experimento de 5%, o p-valor ficou acima da tolerância, indicando que o experimento não é significativo para um nível de 5%. Obviamente, também não é significativo para um nível de 1%.

Logo abaixo do quadro da ANOVA, é apresentado o coeficiente de variação do experimento (CV): 47,83%. O CV é utilizado para medir a precisão do experimento, representado pelo o desvio-padrão expresso como porcentagem da média. A interpretação do CV é muito subjetiva e varia muito entre as áreas da ciência.

Outra informação importante antes de aceitar o resultado da ANOVA, é verificar se os resíduos apresentam normalidade. Esta é uma pressuposição importante, uma vez que valida a escolha do modelo teórico do DIC para explicar o fenômeno:

\[Y = \bar{Y} + TRAT + Erro\]

A não normalidade coloca em xeque o modelo teórico escolhido. Sendo então indicado a transformação dos dados e novo processamento da análise. A pressuposição deve então ser novamente verificada. Obtendo normalidade, os resultados obtidos com a variável transformada podem ser utilizados. Caso contrário, recomenda-se o uso de testes não paramétricos.

Neste exemplo, o teste de normalidade foi não significativo (p-valor = 0,06) e portanto não há evidências para rejeitar a hipótese de normalidade dos resíduos. Lembre-se que a pressuposição de normalidade deve ser sempre analisada em relação aos resíduos, e não às variáveis. A variável apresentar normalidade não garante que os resíduos do modelo estatístico também apresentarão normalidade.

A última parte da saída apresenta o resultado do desdobramento caso o teste F seja significativo. Neste experimento, os tratamentos não são significativos e portanto, apresenta-se apenas a média de cada tratamento.

6.3 Outro caso balanceado

Neste exemplo, segue outro experimento em delineamento inteiramente casualizado, em que se avalia a resposta no desenvolvimento em altura das plantas de quatro níveis de um nutriente. Cada nível de nutriente foi repetido 6 vezes. Assim o experimento pode ser resumido como:

Tratamento: 4 dosagens de um nutriente
6 repetições
Variável de interesse: altura

Table 6.2: Dados de outro delineamento inteiramente casualizado
tratamento	rep	altura
0	1	32.3
0	2	50.6
0	3	50.6
0	4	38.8
0	5	37.1
0	6	26.3
25	1	46.3
25	2	50.3
25	3	47.5
25	4	45.6
25	5	63.9
25	6	36.3
50	1	68.5
50	2	93.9
50	3	96.5
50	4	77.7
50	5	77.7
50	6	68.8
75	1	26.3
75	2	40.3
75	3	37.7
75	4	35.1
75	5	33.9
75	6	26.3

O primeiro passo é importar o arquivo csv contendo os resultados do experimento para dentro do R. Esta tarefa pode ser realizada através do seguinte comando:

dic2 = read.csv("./data/Experimento DIC 2.csv")

Antes de chamar a análise estatística, recomenda-se explorar os dados graficamente. O gráfico permite verificar a tendência da variável altura em função das doses, além de verificar a possível ocorrência de outliers. Por se tratar de um experimento de níveis quantitativos, o gráfico de dispersão é mais adequado:

plot(data = dic2, altura ~ tratamento)

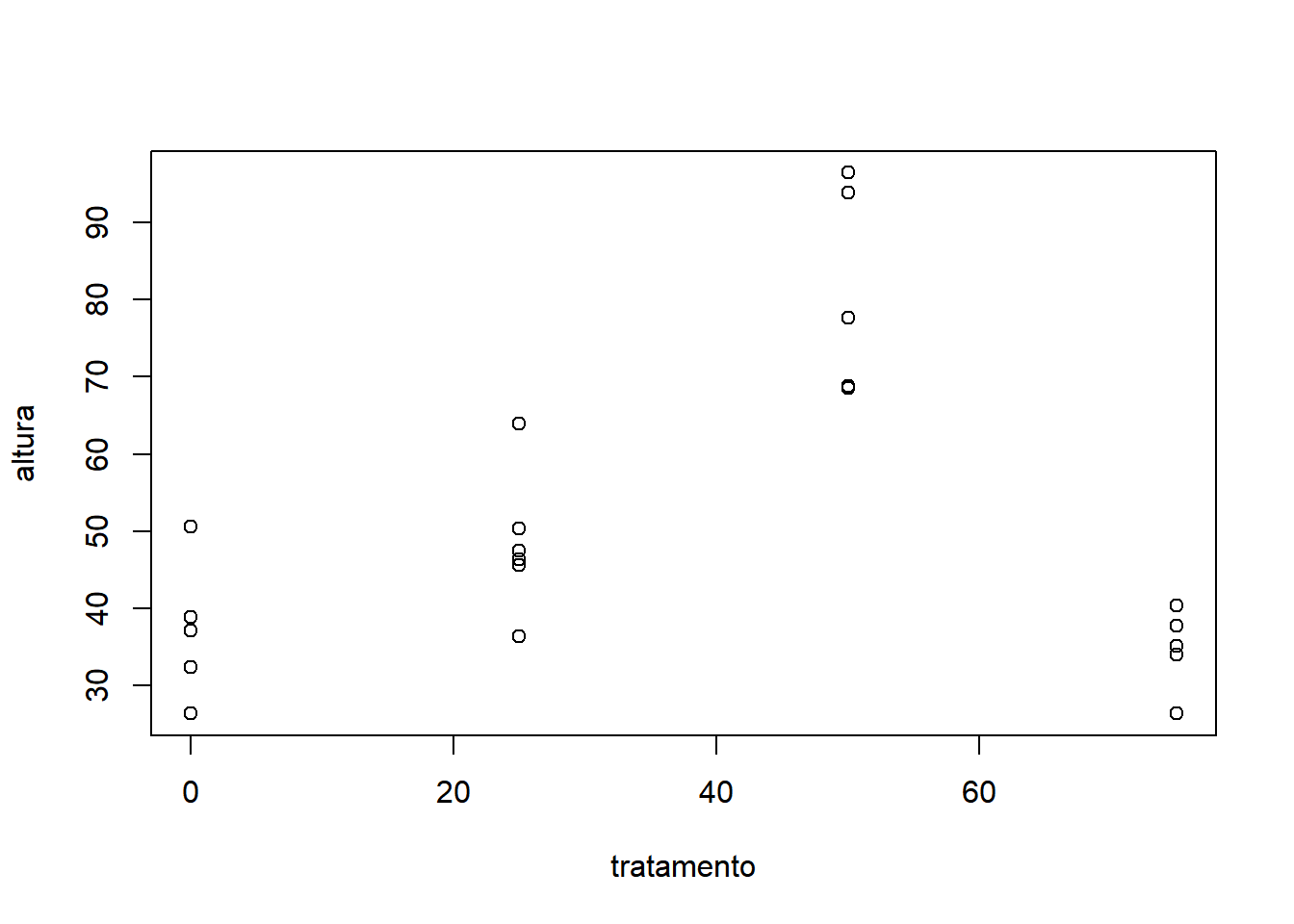
O gráfico indica que a dosagem de 50 apresenta um desenvolvimento em altura superior às demais dosagens. Outro ponto que fica claro com o gráfico, é que o tratamento tem um efeito quadrático sobre a altura. Por se tratar de um caso balanceado, a análise estatística pode ser realizada com a função dic() do pacote ExpDes.pt:

require(ExpDes.pt)
dic(dic2$tratamento, dic2$altura, quali = FALSE)

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL     SQ      QM     Fc     Pr>Fc
## Tratamento  3 7970.8 2656.95 29.789 1.413e-07
## Residuo    20 1783.8   89.19                 
## Total      23 9754.7                         
## ------------------------------------------------------------------------
## CV = 18.76 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos ( Shapiro-Wilk ) 
## Valor-p:  0.1590112 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia 
## valor-p:  0.5117623 
## De acordo com o teste de bartlett a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
## 
## Ajuste de modelos polinomiais de regressao
## ------------------------------------------------------------------------
## 
## Modelo Linear
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  48.2233     3.2258    14.9493    0   
## b1   0.0566     0.0690    0.8206  0.4215 
## -----------------------------------------
## 
## R2 do modelo linear
## --------
## 0.007536
## --------
## 
## Analise de variancia do modelo linear
## ===========================================================
##                      GL     SQ         QM      Fc   valor.p
## -----------------------------------------------------------
## Efeito linear        1   60.0668    60.0668   0.67  0.42152
## Desvios de Regressao 2  7,910.7750 3,955.3870 44.35    0   
## Residuos             20 1,783.8380  89.1919                
## -----------------------------------------------------------
## ------------------------------------------------------------------------
## 
## Modelo quadratico
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  34.1525     3.7579    9.0881     0   
## b1   1.7451     0.2414    7.2292     0   
## b2  -0.0225     0.0031    -7.2990    0   
## -----------------------------------------
## 
## R2 do modelo quadratico
## --------
## 0.603674
## --------
## 
## Analise de variancia do modelo quadratico
## ===========================================================
##                      GL     SQ         QM      Fc   valor.p
## -----------------------------------------------------------
## Efeito linear        1   60.0668    60.0668   0.67  0.42152
## Efeito quadratico    1  4,751.7200 4,751.7200 53.28    0   
## Desvios de Regressao 1  3,159.0540 3,159.0540 35.42  1e-05 
## Residuos             20 1,783.8380  89.1919                
## -----------------------------------------------------------
## ------------------------------------------------------------------------
## 
## Modelo cubico
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  39.2833     3.8556    10.1888    0   
## b1  -1.4702     0.5917    -2.4846 0.0219 
## b2   0.1006     0.0209    4.8101  0.0001 
## b3  -0.0011     0.0002    -5.9514 0.00001
## -----------------------------------------
## 
## R2 do modelo cubico
## -
## 1
## -
## 
## Analise de variancia do modelo cubico
## ===========================================================
##                      GL     SQ         QM      Fc   valor.p
## -----------------------------------------------------------
## Efeito linear        1   60.0668    60.0668   0.67  0.42152
## Efeito quadratico    1  4,751.7200 4,751.7200 53.28    0   
## Efeito cubico        1  3,159.0540 3,159.0540 35.42  1e-05 
## Desvios de Regressao 0      0          0        0      1   
## Residuos             20 1,783.8380  89.1919                
## -----------------------------------------------------------
## ------------------------------------------------------------------------

Note que o comando utilizado é muito semelhante ao exemplo anterior, com apenas uma diferença no parâmetro quali. Neste experimento, utiliza-se o parâmetro como FALSE por se tratar de um experimento com tratamento quantitativo.

O modelo estatístico pode ser aceito uma vez que não há evidências para rejeitar a hipótese de normalidade dos resíduos e homogeneidade de variâncias. Desta forma, pode-se dar sequência na interpretação dos resultados da análise do experimento.

Os tratamentos podem ser considerados significativos já que seu p-valor é inferior a 1%. O desdobramento do tratamento é realizado através de um teste de regressão, já que os níveis do tratamento são quantitativos e deseja-se obter uma equação de regressão que forneça a dose que proporciona a maior altura.

Como padrão, a função dic() desdobra os níveis do tratamento em três modelos: linear, quadrático e cúbico. Pelo gráfico de dispersão criado na fase de exploração dos dados, espera-se que o modelo quadrático seja o mais adequado para representação do experimento.

Com base nos resultados do desdobramento, nota-se que o modelo linear e cúbico são claramente inadequados. No caso do modelo linear, o p-valor indica não significância do efeito linear, reforçado pelo coeficiente de determinação próximo a zero. O efeito cúbico, também foi inadequado pela falta de graus de liberdade. Como experimento analisado conta apenas com 4 níveis no tratamento, não sobra graus de liberdade para o resíduo. O modelo quadrático, por sua vez, apresenta um efeito significativo frente à análise de variância, tanto do efeito quanto dos coeficientes. O coeficiente de determinação de 60,36% também indica um ajuste satisfatório.

A dose ótima do nutriente é de 38,8 gramas, indicado pelo ponto de máximo do modelo quadrático ajustado aos níveis analisados. Cuidado com extrapolações, uma vez que o experimento não contempla doses fora do intervalo analisado.

6.4 O caso desbalanceado

Experimentos desbalanceados são muito comuns na área das ciências agrárias. Isto ocorre principalmente devido à perda unidades experimentais devido à contaminação, morte ou eventos não previstos. Veja o experimento em delineamento inteiramente casualizado, em que se avalia a resposta no desenvolvimento em altura das plantas de quatro níveis de um nutriente. Cada nível de nutriente foi repetido 6 vezes.

Tratamento: 4 dosagens de um nutriente
6 repetições
Variável de interesse: altura

No entanto, perceba que duas medições foram perdidas por morte das plantas:

dose 0 repetição 4
dose 75 repetição 2

Table 6.3: Dados de outro delineamento inteiramente casualizado, porém neste caso desbalanceado
tratamento	rep	altura
0	1	32.3
0	2	50.6
0	3	50.6
0	5	37.1
0	6	26.3
25	1	46.3
25	2	50.3
25	3	47.5
25	4	45.6
25	5	63.9
25	6	36.3
50	1	68.5
50	2	93.9
50	3	96.5
50	4	77.7
50	5	77.7
50	6	68.8
75	1	26.3
75	3	37.7
75	4	35.1
75	5	33.9
75	6	26.3

O primeiro passo é importar o arquivo contendo os resultados do experimento para dentro do R. Esta tarefa pode ser realizada através do seguinte comando:

dic3 = read.csv("./data/Experimento DIC 3.csv")

Antes de chamar a análise estatística, recomenda-se explorar os dados graficamente. Por se tratar de um tratamento de níveis quantitativos, o gráfico de dispersão é mais adequado:

plot(data = dic3, altura ~ tratamento)

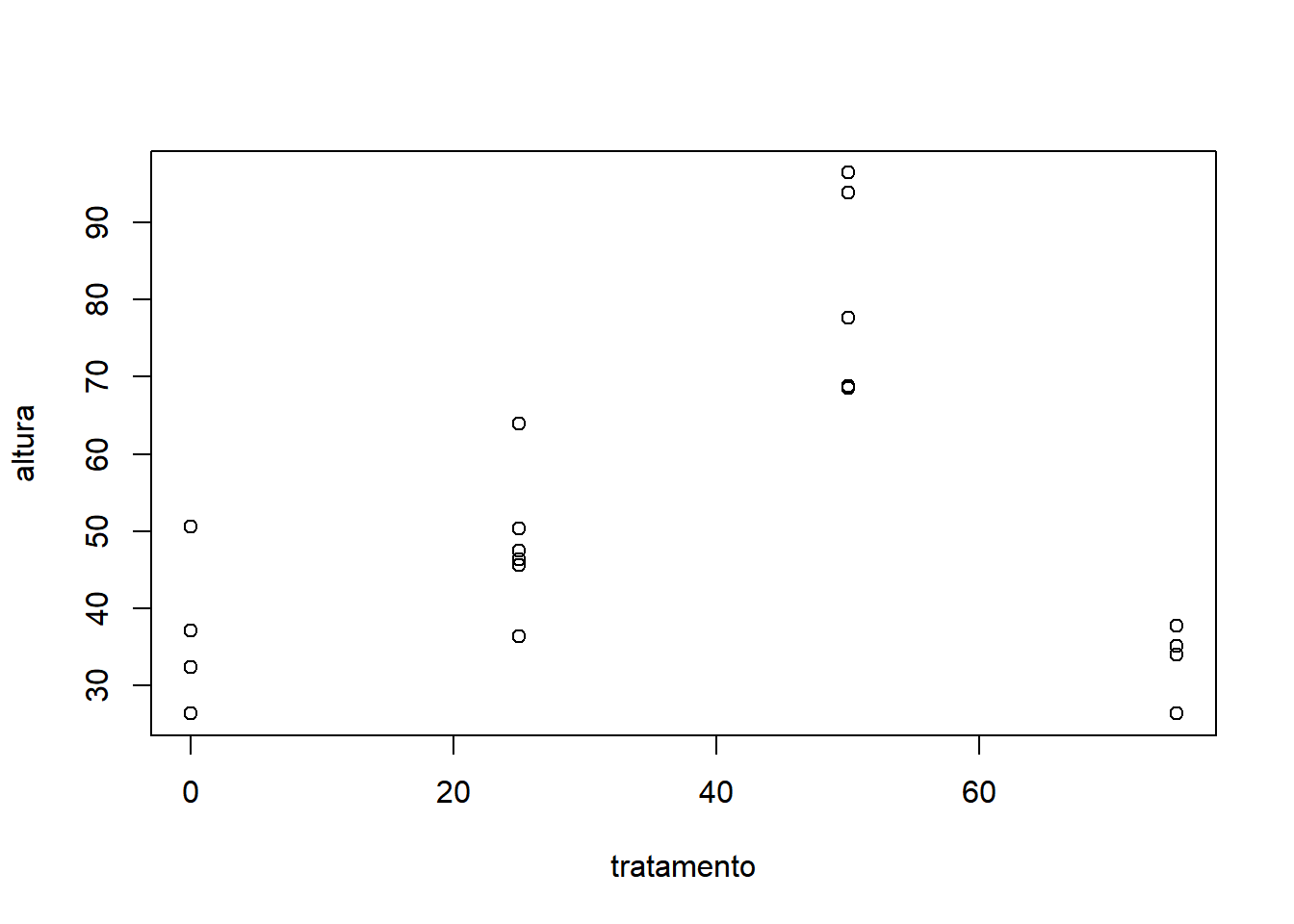
Mesmo se tratando de um experimento desbalanceado, por se tratar de um DIC e consequentemente não existir interações a serem calculadas, pode-se utilizar a ANOVA Tipo I. Com relação aos parâmetros opcionais, apenas o parâmetro quali precisa ser alterado para FALSE, por se tratar tratamento quantitativo:

require(ExpDes.pt)
dic(dic3$tratamento, dic3$altura, quali = FALSE)

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL     SQ      QM     Fc      Pr>Fc
## Tratamento  3 7775.1 2591.69 27.056 6.8921e-07
## Residuo    18 1724.2   95.79                  
## Total      21 9499.3                          
## ------------------------------------------------------------------------
## CV = 19.07 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos ( Shapiro-Wilk ) 
## Valor-p:  0.1497467 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia 
## valor-p:  0.4610355 
## De acordo com o teste de bartlett a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
## 
## Ajuste de modelos polinomiais de regressao
## ------------------------------------------------------------------------
## 
## Modelo Linear
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  48.9626     3.5785    13.6823    0   
## b1   0.0631     0.0775    0.8134  0.4266 
## -----------------------------------------
## 
## R2 do modelo linear
## --------
## 0.008151
## --------
## 
## Analise de variancia do modelo linear
## ===========================================================
##                      GL     SQ         QM      Fc   valor.p
## -----------------------------------------------------------
## Efeito linear        1   63.3741    63.3741   0.66  0.42662
## Desvios de Regressao 2  7,711.6930 3,855.8460 40.25    0   
## Residuos             18 1,724.1970  95.7887                
## -----------------------------------------------------------
## ------------------------------------------------------------------------
## 
## Modelo quadratico
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  33.2553     4.2463    7.8316     0   
## b1   1.7909     0.2631    6.8063     0   
## b2  -0.0230     0.0034    -6.8717    0   
## -----------------------------------------
## 
## R2 do modelo quadratico
## --------
## 0.589904
## --------
## 
## Analise de variancia do modelo quadratico
## ===========================================================
##                      GL     SQ         QM      Fc   valor.p
## -----------------------------------------------------------
## Efeito linear        1   63.3741    63.3741   0.66  0.42662
## Efeito quadratico    1  4,523.1710 4,523.1710 47.22    0   
## Desvios de Regressao 1  3,188.5220 3,188.5220 33.29  2e-05 
## Residuos             18 1,724.1970  95.7887                
## -----------------------------------------------------------
## ------------------------------------------------------------------------
## 
## Modelo cubico
## =========================================
##    Estimativa Erro.padrao   tc    valor.p
## -----------------------------------------
## b0  39.3800     4.3770    8.9971     0   
## b1  -1.4961     0.6275    -2.3840 0.0283 
## b2   0.1019     0.0219    4.6503  0.0002 
## b3  -0.0011     0.0002    -5.7695 0.00002
## -----------------------------------------
## 
## R2 do modelo cubico
## -
## 1
## -
## 
## Analise de variancia do modelo cubico
## ===========================================================
##                      GL     SQ         QM      Fc   valor.p
## -----------------------------------------------------------
## Efeito linear        1   63.3741    63.3741   0.66  0.42662
## Efeito quadratico    1  4,523.1710 4,523.1710 47.22    0   
## Efeito cubico        1  3,188.5220 3,188.5220 33.29  2e-05 
## Desvios de Regressao 0      0          0        0      1   
## Residuos             18 1,724.1970  95.7887                
## -----------------------------------------------------------
## ------------------------------------------------------------------------